物理信息深度学习(PINN)
本文最后更新于：1 个月前
物理信息深度学习(PINN)
偏微分方程的数据驱动解和数据驱动发现 >在 GitHub 上查看 ## 作者 马齐亚·赖西, 巴黎·佩迪卡里斯, 和 乔治·埃姆·卡尼亚达基斯 ## 摘要 我们介绍了物理信息神经网络-神经网络训练解决监督学习任务，同时尊重任何给定的物理定律，由一般非线性偏微分方程描述。我们在解决两类主要问题的背景下提出了我们的发展:偏微分方程的数据驱动解和数据驱动发现。根据可用数据的性质和布局，我们设计了两类不同的算法，即连续时间模型和离散时间模型。由此产生的神经网络形成了一种新的数据高效的通用函数近似器，可以自然地将任何潜在的物理定律编码为先验信息。在第一部分中，我们将演示如何使用这些网络来推断偏微分方程的解，并获得关于所有输入坐标和自由参数的完全可微的物理代理模型。在第二部分，我们重点讨论了偏微分方程的数据驱动发现问题。 ## 非线性偏微分方程的数据驱动解 在我们两部分的论文的第一部分，我们关注于计算一般形式的偏微分方程的数据驱动解 \[u_t + \mathcal{N}[u] = 0,\ x \in \Omega, \ t\in[0,T],\] 其中 \(u(t,x)\)表示潜(隐)解, \(\mathcal{N}[\cdot]\) 是非线性微分算子, \(\Omega\) 是 \(\mathbb{R}^D\) 上的一个数据集。接下来，我们提出了两类不同的算法，即连续时间模型和离散时间模型，并通过不同的基准问题来突出它们的性质和性能。所有代码和数据集都可以在这里找到。 ### 连续时间模型 定义 \(f(t,x)\) 为 \[f := u_t + \mathcal{N}[u],\] 并通过深度神经网络逼近 \(u(t,x)\). 这个假设产生了一个物理信息的神经网络 \(f(t,x)\). 这个网络可以通过计算图的演算得到:反向传播。
示例（Burgers方程)
举个例子，让我们考虑 Burgers 方程。在一维空间中，考虑带有 Dirichlet 边界的Burgers方程 \[ \begin{array}{l} u_t + u u_x - (0.01/\pi) u_{xx} = 0,\ \ \ x \in [-1,1],\ \ \ t \in [0,1],\\ u(0,x) = -\sin(\pi x),\\ u(t,-1) = u(t,1) = 0. \end{array} \]
定义 \(f(t,x)\) 为 \[f := u_t + u u_x - (0.01/\pi) u_{xx},\] 并通过深度神经网络逼近 \(u(t,x)\). 为了强调实现这个想法的简单性，使用 Tensorflow 包给出一个 Python 代码片段。为此，\(u(t,x)\) 可以简单地定义为 1
2
3def u(t, x):
u = neural_net(tf.concat([t,x],1), weights, biases)
return u1
2
3
4
5
6
7def f(t, x):
u = u(t, x)
u_t = tf.gradients(u, t)[0]
u_x = tf.gradients(u, x)[0]
u_xx = tf.gradients(u_x, x)[0]
f = u_t + u*u_x - (0.01/tf.pi)*u_xx
return f
\[MSE_f = \frac{1}{N_f}\sum_{i=1}^{N_f}|f(t_f^i,x_f^i)|^2.\] 这里, \(\{t_u^i, x_u^i, u^i\}_{i=1}^{N_u}\) 表示 \(u(t,x)\) 的初始和边界训练数据和指定 \(f(t,x)\) 的配置点\(\{t_f^i, x_f^i\}_{i=1}^{N_f}\). 损失 \(MSE_u\) 对应于初始和边界数据，而 \(MSE_f\) 在有限的配置点集上强制执行 Burgers 方程强加的结构。
下图总结了我们在数据驱动下求解 Burgers 方程的结果。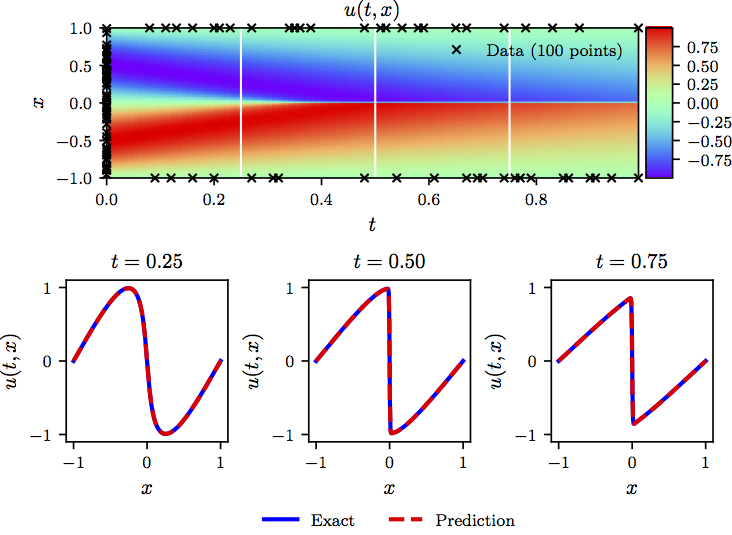 
>Burgers 方程: Top: 预测解连同初始和边界训练数据。此外，我们还使用了10,000个使用拉丁超立方抽样策略生成的搭配点。 Bottom: 顶部图片中白色垂直线描绘的三个时间快照对应的预测解和精确解的比较。在单个 NVIDIA Titan X GPU 卡上进行模型训练大约需要 60 秒。 > 示例 (Shrödinger 方程)
此示例旨在强调我们的方法处理周期性边界条件、复值解以及控制偏微分方程中不同类型非线性的能力。非线性薛定谔方程以及周期性边界条件由下式给出 \[\begin{array}{l} i h_t + 0.5 h_{xx} + |h|^2 h = 0,\ \ \ x \in [-5, 5],\ \ \ t \in [0, \pi/2],\\ h(0,x) = 2\ \text{sech}(x),\\ h(t,-5) = h(t, 5),\\ h_x(t,-5) = h_x(t, 5), \end{array}\] 其中 \(h(t,x)\) 是复值解. 定义 \(f(t,x)\) 为 \[f := i h_t + 0.5 h_{xx} + |h|^2 h,\] 并将复值神经网络置于 \(h(t,x)\). 事实上，如果 \(u\) 表示 \(h\) 的实部而 \(v\) 是虚部，我们放置了一个多出神经网络 \(h(t,x) = \begin{bmatrix} u(t,x) \\ v(t,x) \end{bmatrix}\). 这将得到复值(多输出)物理信息神经网络\(f(t,x)\)。 神经网络 \(h(t,x)\) 和 \(f(t,x)\) 的共享参数可以通过最小化均方误差损失来学习 \[MSE = MSE_0 + MSE_b + MSE_f,\] 其中 \[MSE_0 = \frac{1}{N_0}\sum_{i=1}^{N_0} |h(0,x_0^i) - h^i_0|^2,\] \[MSE_f = \frac{1}{N_f}\sum_{i=1}^{N_f}|f(t_f^i,x_f^i)|^2.\] 这里, \(\{x_0^i, h^i_0\}_{i=1}^{N_0}\) 表示初始数据, \(\{t^i_b\}_{i=1}^{N_b}\) 对应到边界上的搭配点, \(\{t_f^i,x_f^i\}_{i=1}^{N_f}\) 代表 \(f(t,x)\)上的配置点. 因此, \(MSE_0\) 对应于初始数据的损失, \(MSE_b\) 强制执行周期性边界条件,而 \(MSE_f\) 惩罚不满足 Shrödinger 方程的配置点.
下图总结了我们的实验结果。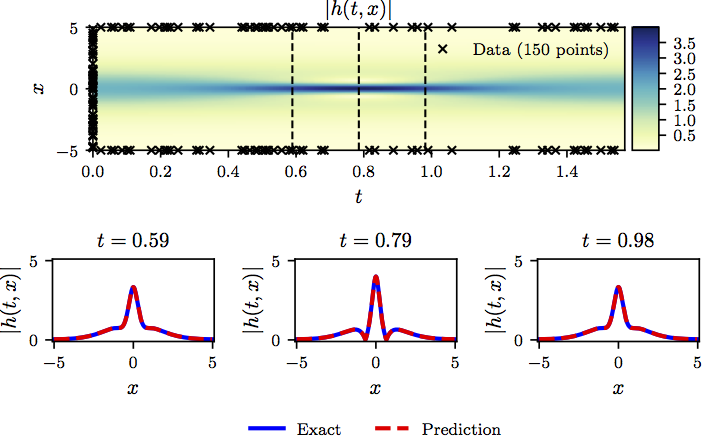 
>Shrödinger 方程: Top: 预测解连同初始和边界训练数据。此外，我们还使用了使用拉丁超立方体采样策略生成的20,000个搭配点. Bottom: 顶部图片中垂直虚线描绘的三个时间快照对应的预测解和精确解的比较。 > 到目前为止所考虑的连续时间神经网络模型的一个潜在限制源于需要使用大量搭配点 \(N_f\) 以在整个时空域中强制执行物理信息约束。虽然这对一维或二维空间的问题没有造成重大问题，但它可能会在高维问题中引入严重的瓶颈，因为全局强制执行物理信息约束所需的配置点总数（即在我们的情况下为偏微分方程）将呈指数增长。在下一节中，我们提出了一种不同的方法，该方法通过利用经典的 Runge-Kutta 时间步进方案引入更结构化的神经网络表示来规避对配置点的需求。
离散时间模型
让我们利用\(q\)阶龙格-库塔方法的一般形式，得到 \[\begin{array}{ll} u^{n+c_i} = u^n - \Delta t \sum_{j=1}^q a_{ij} \mathcal{N}[u^{n+c_j}], \ \ i=1,\ldots,q,\\ u^{n+1} = u^{n} - \Delta t \sum_{j=1}^q b_j \mathcal{N}[u^{n+c_j}]. \end{array}\] 这里, \(u^{n+c_j}(x) = u(t^n + c_j \Delta t, x)\) 对于 \(j=1, \ldots, q\). 这种通用形式封装了隐式和显式时间步进方案，具体取决于参数 \(\{a_{ij},b_j,c_j\}\). 的选择。上面的方程可以等价地表示为 \[\begin{array}{ll} u^{n} = u^n_i, \ \ i=1,\ldots,q,\\ u^n = u^n_{q+1}, \end{array}\] 其中 \[\begin{array}{ll} u^n_i := u^{n+c_i} + \Delta t \sum_{j=1}^q a_{ij} \mathcal{N}[u^{n+c_j}], \ \ i=1,\ldots,q,\\ u^n_{q+1} := u^{n+1} + \Delta t \sum_{j=1}^q b_j \mathcal{N}[u^{n+c_j}]. \end{array}\] 我们先放置一个多输出神经网络 \[\begin{bmatrix} u^{n+c_1}(x), \ldots, u^{n+c_q}(x), u^{n+1}(x) \end{bmatrix}.\] 这个先验假设加上上面的方程式得到了一个以\(x\)作为输入和输出的物理信息神经网络 \[\begin{bmatrix} u^n_1(x), \ldots, u^n_q(x), u^n_{q+1}(x) \end{bmatrix}.\]
示例 (Allen-Cahn 方程) 这个例子旨在强调提出的离散时间模型处理控制偏微分方程中不同类型非线性的能力。为此目的，让我们考虑 Allen-Cahn 方程和周期边界条件 \[\begin{array}{l} u_t - 0.0001 u_{xx} + 5 u^3 - 5 u = 0, \ \ \ x \in [-1,1], \ \ \ t \in [0,1],\\ u(0, x) = x^2 \cos(\pi x),\\ u(t,-1) = u(t,1),\\ u_x(t,-1) = u_x(t,1). \end{array}\] Allen-Cahn 方程是反应扩散系统领域的一个著名方程。它描述了多组分合金体系的相分离过程，包括有序-无序转变。对于 Allen-Cahn 方程，给出了非线性算子 \[\mathcal{N}[u^{n+c_j}] = -0.0001 u^{n+c_j}_{xx} + 5 \left(u^{n+c_j}\right)^3 - 5 u^{n+c_j},\] 并且可以通过最小化误差平方和来学习神经网络的共享参数 \[SSE = SSE_n + SSE_b,\] 其中 \[SSE_n = \sum_{j=1}^{q+1} \sum_{i=1}^{N_n} |u^n_j(x^{n,i}) - u^{n,i}|^2,\] \[% <![CDATA[ \begin{array}{rl} SSE_b =& \sum_{i=1}^q |u^{n+c_i}(-1) - u^{n+c_i}(1)|^2 + |u^{n+1}(-1) - u^{n+1}(1)|^2 \\ +& \sum_{i=1}^q |u_x^{n+c_i}(-1) - u_x^{n+c_i}(1)|^2 + |u_x^{n+1}(-1) - u_x^{n+1}(1)|^2. \end{array} %]]>\] 这里, \(\{x^{n,i}, u^{n,i}\}_{i=1}^{N_n}\) 对应于时间 \(t^n\) 的数据.
下图总结了我们使用上述损失函数训练网络后的预测结果。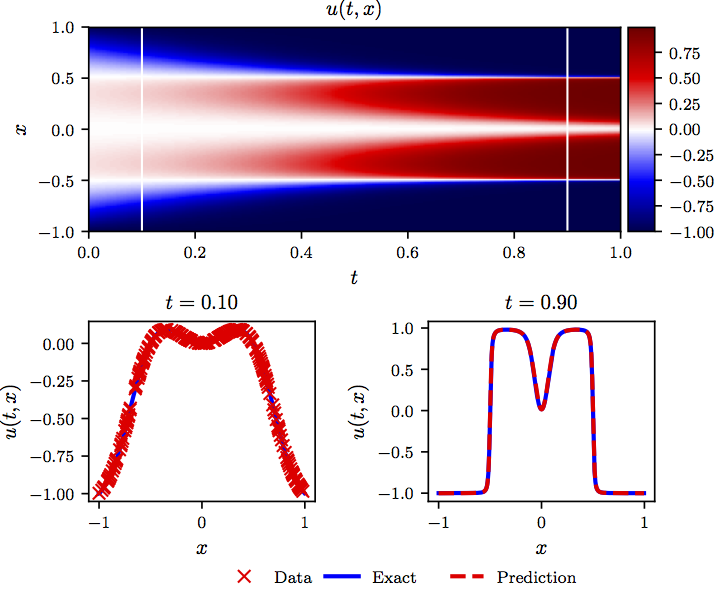 
>Allen-Cahn 方程: Top: 解以及初始训练(t=0.1)到最终预测(t=0.9)训练快照的位置. Bottom: 顶部图片中白色垂直线描绘的初始训练数据和最终预测快照。
非线性偏微分方程的数据驱动发现
在我们研究的第二部分，我们将注意力转移到偏微分方程的数据驱动发现问题。为此，我们考虑一般形式的参数化非线性偏微分方程 \[u_t + \mathcal{N}[u;\lambda] = 0,\ x \in \Omega, \ t\in[0,T],\] 其中 \(u(t,x)\) 表示潜在（隐藏）解, \(\mathcal{N}[\cdot;\lambda]\) 是由 \(\lambda\) 参数化的非线性算子, \(\Omega\) 是 \(\mathbb{R}^D\) 上的数据集.现在，数据驱动的偏微分方程发现问题提出了以下问题:给定一个小的分散的和潜在的噪声观测的隐藏状态 \(u(t,x)\)，什么参数 \(\lambda\) 能够最好地描述观测数据?
在下文中，我们将概述我们解决这个问题的两种主要方法，即连续时间模型和离散时间模型，以及针对各种基准集合的一系列结果和系统研究。在第一种方法中，我们将假设在整个时空域中可以使用分散的和潜在的噪声测量。 在后者中，我们将尝试仅从在不同时刻拍摄的两个数据快照推断未知参数 \(\lambda\)。本手稿中使用的所有数据和代码均可在 GitHub 上公开获取. ### 连续时间模型 定义 \(f(t,x)\) 为 \[f := u_t + \mathcal{N}[u;\lambda],\label{eq:PDE_RHS}\] 然后通过深度神经网络逼近 \(u(t,x)\). 这个假设生成了一个物理信息神经网络 \(f(t,x)\). 这个网络可以通过计算图的演算得到:反向传播。值得强调的是，微分算子 \(\lambda\) 的参数变成了物理信息神经网络 \(f(t,x)\) 的参数。
示例 (Navier-Stokes 方程)
我们的下一个例子涉及不可压缩流体流动的现实场景，如无处不在的Navier-Stokes方程所描述的。 Navier-Stokes 方程描述了许多科学和工程感兴趣的物理学现象。它们可以用来模拟天气、洋流、管道中的水流和机翼周围的空气流动。 Navier-Stokes 方程的完整和简化形式有助于飞机和汽车的设计、血液流动的研究、电站的设计、污染物扩散的分析和许多其他应用。让我们考虑二维(2D)的 Navier-Stokes 方程 \[\begin{array}{c} u_t + \lambda_1 (u u_x + v u_y) = -p_x + \lambda_2(u_{xx} + u_{yy}),\\ v_t + \lambda_1 (u v_x + v v_y) = -p_y + \lambda_2(v_{xx} + v_{yy}), \end{array}\] 其中 \(u(t, x, y)\) 表示速度场的 \(x\)-分量，\(v(t, x, y)\) 表示 \(y\)-分量，\(p(t, x, y)\) 表示压力。这里，\(\lambda = (\lambda_1, \lambda_2)\) 是未知参数。在无散度函数集中搜索Navier-Stokes 方程的解;也就是说 \[u_x + v_y = 0.\] 这个额外的方程是不可压缩流体的连续方程，它描述了流体的质量守恒。我们假设 \[u = \psi_y,\ \ \ v = -\psi_x,\] 对于某些潜在函数 \(\psi(t,x,y)\)。在这个假设下，连续性方程将自动得到满足。给定噪声测量 \[\{t^i, x^i, y^i, u^i, v^i\}_{i=1}^{N}\] 对于速度场，我们感兴趣的是参数 \(\lambda\) 以及压力 \(p(t,x,y)\). 定义 \(f(t,x,y)\) 和 \(g(t,x,y)\) 为 \[\begin{array}{c} f := u_t + \lambda_1 (u u_x + v u_y) + p_x - \lambda_2(u_{xx} + u_{yy}),\\ g := v_t + \lambda_1 (u v_x + v v_y) + p_y - \lambda_2(v_{xx} + v_{yy}), \end{array}\] 然后使用具有两个输出的单个神经网络联合逼近 \(\begin{bmatrix} \psi(t,x,y) \\ p(t,x,y) \end{bmatrix} %\). 这个先验假设得到了一个物理信息的神经网络\(\begin{bmatrix} f(t,x,y) \\ g(t,x,y) \end{bmatrix}\). Navier-Stokes 算子的参数 \(\lambda\) 以及神经网络的参数 \(\begin{bmatrix} \psi(t,x,y) \\ p(t,x,y) \end{bmatrix}\) 和 \(\begin{bmatrix} f(t,x,y) \\ g(t,x,y) \end{bmatrix}\) 可以通过最小化均方误差损失来训练 \[% <![CDATA[ \begin{array}{rl} MSE :=& \frac{1}{N}\sum_{i=1}^{N} \left(|u(t^i,x^i,y^i) - u^i|^2 + |v(t^i,x^i,y^i) - v^i|^2\right) \\ +& \frac{1}{N}\sum_{i=1}^{N} \left(|f(t^i,x^i,y^i)|^2 + |g(t^i,x^i,y^i)|^2\right). \end{array} %]]>\]
下图显示了我们在此示例中的结果摘要。
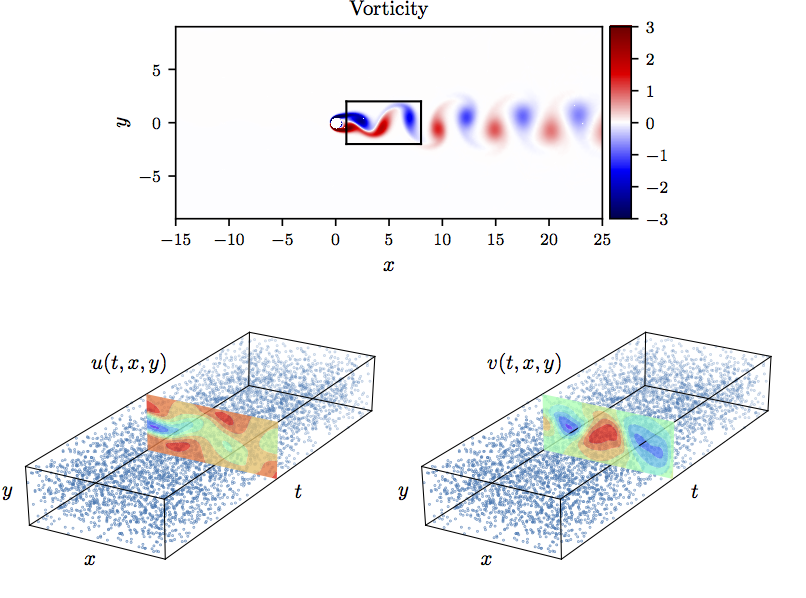>Navier-Stokes 方程: Top: Re=100时，不可压缩流动和动态涡脱落经过圆柱体。时空训练数据对应于圆柱体尾流中所描绘的矩形区域. Bottom: 流向和横向速度分量的训练数据点的位置。.
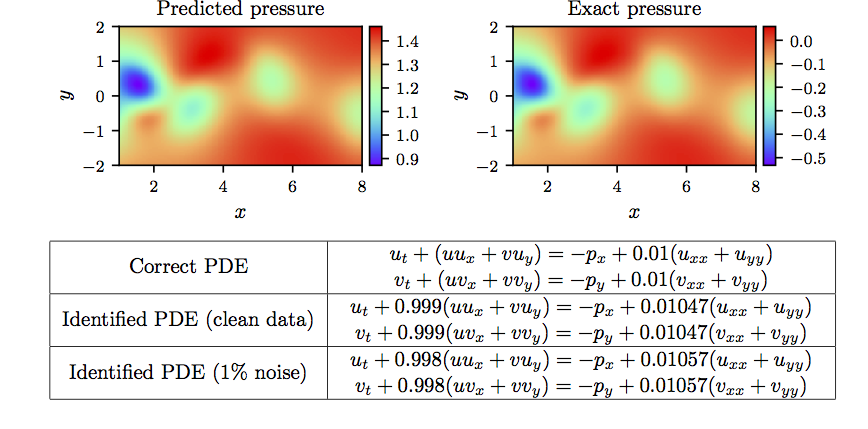>Navier-Stokes 方程: Top: 代表时刻的预测与精确瞬时压力场。根据定义，压力可以恢复到一个常数，从而证明两个图之间的不同幅度是合理的。这种显着的定性一致性突出了基于物理的神经网络在模型训练期间没有使用压力数据而识别整个压力场的能力。Bottom: 对偏微分方程进行了修正.
到目前为止，我们的方法是假设在整个时空域都可以获得分散的数据。然而，在许多实际感兴趣的情况下，人们可能只能在不同的时间瞬间观察系统。在下一节中，我们将介绍一种不同的方法，它只使用两个数据快照来处理数据驱动的发现问题。我们将看到，如何利用经典的龙格-库塔时间步进方案，构建离散时间物理信息神经网络，即使在数据快照之间的时间差距非常大的情况下，也能保持高预测精度。 ### 离散时间模型
我们首先采用 \(q\) 阶龙格-库塔方法的一般形式，得到 \[\begin{array}{ll} u^{n+c_i} = u^n - \Delta t \sum_{j=1}^q a_{ij} \mathcal{N}[u^{n+c_j};\lambda], \ \ i=1,\ldots,q,\\ u^{n+1} = u^{n} - \Delta t \sum_{j=1}^q b_j \mathcal{N}[u^{n+c_j};\lambda]. \end{array}\] 这里, \(u^{n+c_j}(x) = u(t^n + c_j \Delta t, x)\) 对于 \(j=1, \ldots, q\). 这种通用形式封装了隐式和显式时间步进方案，具体取决于参数 \(\{a_{ij},b_j,c_j\}\). 的选择。上面的方程可以等价地表示为 \[\begin{array}{ll} u^{n} = u^n_i, \ \ i=1,\ldots,q,\\ u^{n+1} = u^{n+1}_{i}, \ \ i=1,\ldots,q. \end{array}\] 其中 \[\begin{array}{ll} u^n_i := u^{n+c_i} + \Delta t \sum_{j=1}^q a_{ij} \mathcal{N}[u^{n+c_j};\lambda], \ \ i=1,\ldots,q,\\ u^{n+1}_{i} := u^{n+c_i} + \Delta t \sum_{j=1}^q (a_{ij} - b_j) \mathcal{N}[u^{n+c_j};\lambda], \ \ i=1,\ldots,q. \end{array}\] 我们先放置一个多输出神经网络 \[\begin{bmatrix} u^{n+c_1}(x), \ldots, u^{n+c_q}(x) \end{bmatrix}.\] 这一先验假设产生了两个物理信息神经网络 \[\begin{bmatrix} u^{n}_1(x), \ldots, u^{n}_q(x), u^{n}_{q+1}(x) \end{bmatrix},\] 和 \[\begin{bmatrix} u^{n+1}_1(x), \ldots, u^{n+1}_q(x), u^{n+1}_{q+1}(x) \end{bmatrix}.\] 给定两个不同时间快照的噪声测量值 \(\{\mathbf{x}^{n}, \mathbf{u}^{n}\}\) 和 \(\{\mathbf{x}^{n+1}, \mathbf{u}^{n+1}\}\) 系统的时间分别为 \(t^{n}\) 和 \(t^{n+1}\), 神经网络的共享参数以及微分算子的参数 \(\lambda\) 可以通过最小化误差平方和来训练 \[SSE = SSE_n + SSE_{n+1},\] 其中 \[SSE_n := \sum_{j=1}^q \sum_{i=1}^{N_n} |u^n_j(x^{n,i}) - u^{n,i}|^2,\] \[SSE_{n+1} := \sum_{j=1}^q \sum_{i=1}^{N_{n+1}} |u^{n+1}_j(x^{n+1,i}) - u^{n+1,i}|^2.\] 这里, \(\mathbf{x}^n = \left\{x^{n,i}\right\}_{i=1}^{N_n}\), \(\mathbf{u}^n = \left\{u^{n,i}\right\}_{i=1}^{N_n}\), \(\mathbf{x}^{n+1} = \left\{x^{n+1,i}\right\}_{i=1}^{N_{n+1}}\), \(\mathbf{u}^{n+1} = \left\{u^{n+1,i}\right\}_{i=1}^{N_{n+1}}\).
示例 (Korteweg–de Vries 方程)
我们的最后一个例子旨在强调所提出的框架处理涉及高阶导数的控制偏微分方程的能力。在这里，我们考虑浅水表面波的数学模型； Korteweg-de Vries (KdV) 方程。 KdV 方程是 \[u_t + \lambda_1 u u_x + \lambda_2 u_{xxx} = 0,\] 其中 \((\lambda_1, \lambda_2)\) 是未知参数。对于 KdV 方程，非线性算子由下式给出 \[\mathcal{N}[u^{n+c_j}] = \lambda_1 u^{n+c_j} u^{n+c_j}_x - \lambda_2 u^{n+c_j}_{xxx}\] 以及神经网络的共享参数以及 KdV 方程中的参数 \(\lambda = (\lambda_1, \lambda_2)\) 可以通过最小化上面给出的误差平方和来学习。
实验结果总结如下图所示。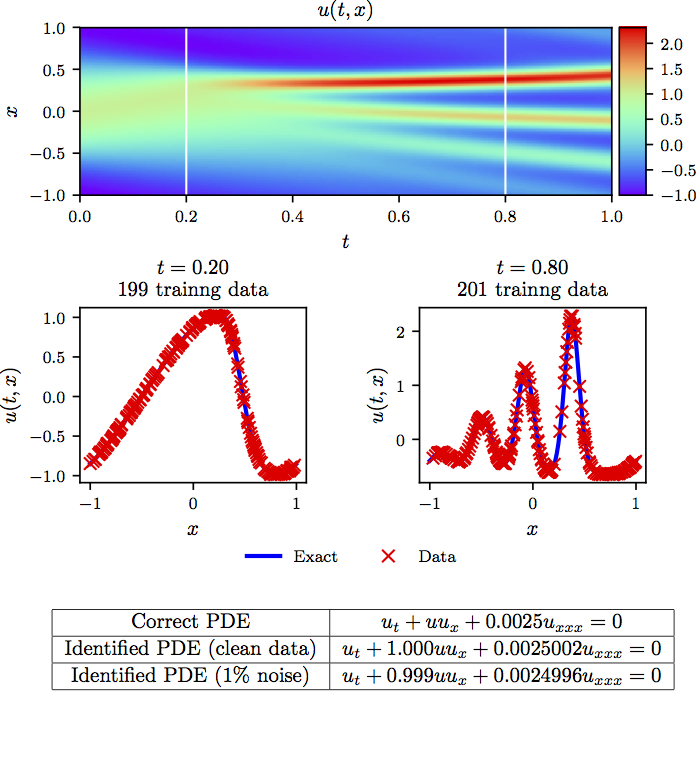 
>KdV 方程n: Top: 解以及两个训练快照的时间位置. Middle: 上图中虚线所示的两个瞬时快照对应的训练数据和精确解. Bottom: 修正偏微分方程以及确定的方程
结论
尽管提出了一系列有希望的结果，但读者可能会同意，这本由两部分组成的论文提出的问题多于它的答案。在更广泛的背景下，并在寻求进一步了解这些工具的过程中，我们相信这项工作倡导机器学习和经典计算物理学之间富有成效的协同作用，有可能丰富这两个领域并导致高影响力的发展。
致谢
这项工作得到了 DARPA EQUiPS 赠款 N66001-15-2-4055 和 AFOSR 赠款 FA9550-17-1-0013 的支持。所有数据和代码都在 GitHub 上公开提供
引文
@article{raissi2019physics, title={Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations}, author={Raissi, Maziar and Perdikaris, Paris and Karniadakis, George E}, journal={Journal of Computational Physics}, volume={378}, pages={686--707}, year={2019}, publisher={Elsevier} }
@article{raissi2017physicsI, title={Physics Informed Deep Learning (Part I): Data-driven Solutions of Nonlinear Partial Differential Equations}, author={Raissi, Maziar and Perdikaris, Paris and Karniadakis, George Em}, journal={arXiv preprint arXiv:1711.10561}, year={2017} }
@article{raissi2017physicsII, title={Physics Informed Deep Learning (Part II): Data-driven Discovery of Nonlinear Partial Differential Equations}, author={Raissi, Maziar and Perdikaris, Paris and Karniadakis, George Em}, journal={arXiv preprint arXiv:1711.10566}, year={2017} }
本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！