常微分方程的解析解(方法归纳)以及基于Python的微分方程数值解算例实现
本文最后更新于：1 个月前
常微分方程的解析解(方法归纳)以及基于Python的微分方程数值解算例实现
本文归纳常见常微分方程的解析解解法以及基于Python的微分方程数值解算例实现。 [toc]
常微分方程的解析解
考虑常微分方程的解析解法，我们一般可以将其归纳为如下几类： 1. 可分离变量的微分方程（一阶） 2. 一阶齐次（非齐次）线性微分方程（一阶） 3. 二阶常系数微分方程（二阶） 4. 高阶常系数微分方程（\(n\)阶） --- ### 可分离变量的微分方程（一阶） 这类微分方程可以变形成如下形式： \[f(x)dx=g(y)dy\] 两边同时积分即可解出函数，难点主要在于不定积分，是最简单的微分方程。
某些方程看似不可分离变量，但是经过换元之后，其实还是可分离变量的，不要被这种方程迷惑。
| ### 一阶齐次（非齐次）线性微分方程（一阶） 形如 \[\frac{dy}{dx}+P(x)y=Q(x) \] 的方程叫做一阶线性微分方程，若\(Q(x)\)为0，则方程齐次，否则称为非齐次。 |
|---|
| ### 二阶常系数微分方程（二阶） 形如 \[y''+py'+qy=f(x)\] 的方程称为二阶常系数微分方程，若\(f(x)\equiv0\)，则方程称为齐次的，反之称为非齐次的。以下默认方程是非齐次的。 |
| 求解此类方程分两步： 1. 求出齐次通解 2. 求出非齐次特解 |
原方程的解=齐次通解+非齐次特解 * 齐次通解的求法 |
| 首先假设 \(f(x)\equiv0\).用特征方程法，写出对应的特征方程并且求解： \[\lambda^2+p\lambda+q=0\] 解的情况分为以下三种： |
情况一：方程有两个不同的实数解 |
假设两个实数解分别是 \(\lambda_1、\lambda_2\), 此时方程的通解是 \[Y(x)=C_{1}e^{\lambda_1x}+C_{2}e^{\lambda_2x}\] 情况二：方程有一个二重解 假设该解等于\(\lambda\)，此时方程的通解是 \[Y(x)=(C_{1}+C_{2}x)e^{\lambda x}\] 情况三：方程有一对共轭复解 假设这对解是 \(\alpha\pm i\beta\), 此时方程的通解是 \[Y(x)=e^{\alpha x}(C_{1}cos(\beta x)+C_{2}sin(\beta x))\] * 非齐次特解的求法 |
| 对于 \(f(x)\) 和特征根的情况，对特解的情况做如下归纳： |
| 1. \(f(x)=P_{m}(x)\)，其中 \(P_{m}(x)\) 表示 \(x\) 的最高次数为 \(m\) 的多项式。 |
| 若0不是方程特征解 |
| 则方程有特解 \(y^{*}=Q_{m}(x)\) |
| 若0是方程的单特征解 |
| 则方程有特解 \(y^{*}=xQ_{m}(x)\) |
| 若0是方程的二重特征解 |
| 则方程有特解 \(y^{*}=x^{2}Q_{m}(x)\) |
| 其中 \(Q_{m}(x)=b_{0}+b_{1}x+…+b_{m}x^{m}\), \(b_{i}(i = 0,1,…,m)\)是需要带回原方程来确定的系数。 |
| 1. \(f(x)=e^{\alpha x}P_{m}(x)\) |
| 若 \(\alpha\) 不是方程特征解 |
| 则方程有特解 \(y^{*}=e^{\alpha x}Q_{m}(x)\) |
| 若 \(\alpha\) 是方程的单特征解 |
| 则方程有特解 \(y^{*}=xe^{\alpha x}Q_{m}(x)\) |
| 若 \(\alpha\) 是方程的二重特征解 |
| 则方程有特解 \(y^{*}=x^2e^{\alpha x}Q_{m}(x)\) 1. $f(x)=e^{x}(a_{1}cos(x)+a_{2}sin(x)) $ |
| 若 \(\alpha\pm i\beta\) 不是特征解 |
| 则方程有特解 \(y^{*}=e^{\alpha x}(A_{1}cos(\beta x)+A_{2}sin(\beta x))\) |
| 若 \(\alpha\pm i\beta\) 是特征解 |
| 则方程有特解 \(y^{*}=xe^{\alpha x}(A_{1}cos(\beta x)+A_{2}sin(\beta x))\) |
| 其中 \(A_{1}、A_{2}\) 是需要带回原方程来确定的系数。 |
高阶常系数微分方程（n阶）
形如 \[y^{(n)}+p_{1}y^{(n-1)}+...+p_{n-1}y'+p_{n}y=f(x)\] 的方程叫做高阶常系数微分方程，若 \(f(x)\equiv0\)，则方程是齐次的，否则是非齐次的。下面默认方程是非齐次的。
求解此类方程分两步： 1. 求出齐次通解 2. 求出非齐次特解
原方程的解=齐次通解+非齐次特解 * 齐次通解的求法(参考二阶常系数微分方程解法) * 非齐次特解的求法(参考二阶常系数微分方程解法) ---
算例
考虑带有第三类边界条件的二阶常系数微分方程边值问题 \[ \left\{ \begin{aligned} y''(x)+2y'(x)-3y(x) & = 3x+1, & x\in [1,2]\\ y'(1)-y(1) & = 1,\\ y'(2)-y(2) & = -4. \end{aligned} \right. \] 1. 求出上述两点边值问题的解析解; 2. 通过有限差分方法算出其数值解;(取\(h=\frac{1}{5}\))并计算误差、绘图、输出\(1.0,1.2,1.4,1.6,1.8,2.0\)处的数值解.
| 问题一:两点边值问题的解析解 |
| 由于此方程是非齐次的,故求解此类方程分两步： 1. 求出齐次通解 2. 求出非齐次特解 |
原方程的解=齐次通解+非齐次特解 * 齐次通解的求法 |
| 首先假设 \(y''(x)+2y'(x)-3y(x)\equiv0\). 用特征方程法，写出对应的特征方程 \[\lambda^2+2\lambda-3=0\] 求解得到两个不同的实数特征根:\(\lambda_1=1,\lambda_2=-3\). |
| 此时方程的齐次通解是 \[y(x)=C_{1}e^{\lambda_1x}+C_{2}e^{\lambda_2x}\] * 非齐次特解的求法 |
| 由于 \(\lambda_1\ne0,\lambda_2\ne0\). 所以非齐次特解形式为 \[y^{*}=ax+b\] 将上式代入控制方程有 \[2a-3ax-3b=3x+1\] 求解得: \(a=b=-1\), 即非齐次特解为 \(y^{*}=-x-1\). |
原方程的解=齐次通解+非齐次特解 |
| 于是,原方程的全解为 \[y(x)=C_{1}e^{x}+C_{2}e^{-3x}-x-1\] 因为该问题给出的是第三类边界条件,故需要求解的导函数 \[y'(x)=C_{1}e^{x}-3C_{2}e^{-3x}-1\] 且有 \[ \left\{ \begin{aligned} y(1)&=C_1e+C_2e^{-3}-2\\ y'(1)&=C_1e-3C_2e^{-3}-1\\ y(2)&=C_1e^2+C_2e^{-6}-3\\ y'(2)&=C_1e^2-3C_2e^{-6}-1 \end{aligned} \right. \] 将以上各式代入边界条件 \[\left\{ \begin{aligned} y'(1)-y(1)&=-4C_2e^{-3}+1=1\\ y'(2)+y(2)&=2C_1e^2-2C_2e^{-6}-4=-4 \end{aligned} \right. \] 解此方程组可得: \(C_1=C_2=0\). |
| 综上所述,原两点边值问题的解为 \[y=-x-1\] |
| ## 常微分方程的数值解 ### 一般二阶线性常微分方程边值问题的差分法 |
| 对一般的二阶微分方程边值问题 \[ \left\{\begin{array}{l} y^{\prime \prime}(x)+p(x) y^{\prime}(x)+q(x) y(x)=f(x), \quad a<x<b \\ a_{1} y(a)+a_{2} y^{\prime}(a)=a \\ \beta_{1} y(b)+\beta_{2} y^{\prime}(b)=\beta \end{array}\right. \] 假定其解存在唯一, 为求解的近似值, 类似于前面的做法, |
| 1. 把区间 \(I=[a, b] N\) 等分, 即得到区间 \(I=[a, b]\) 的一个网格剖分: \[ a=x_{0}<x_{1}<\cdots<x_{N-1}<x_{N}=b \] 其中分点 \(x_{i}=a+i h(i=0,1, \cdots, N)\), 步长 \(h=\frac{b-a}{N}\). |
| 2. 对式中的二阶导数仍用数值微分公式 \[ y^{\prime \prime}\left(x_{i}\right)=\frac{y\left(x_{i+1}\right)-2 y\left(x_{i}\right)+y\left(x_{i-1}\right)}{h^{2}}-\frac{h^{2}}{12} y^{(4)}\left(\xi_{i}\right), \quad x_{i-1}<\xi_{i}<x_{i} \] 代替，而对一阶导数，为了保证略去的逼近误差为\(O(h^2)\)，则用 3 点数值微分公式；另外为了保证内插，在 2 个端点所用的 3 点数值微分公式与内网格点所用的公式不同，即 \[ \left\{\begin{array}{l} y^{\prime}\left(x_{i}\right)=\frac{y\left(x_{i+1}\right)-y\left(x_{i-1}\right)}{2 h}-\frac{h^{2}}{6} y^{\prime \prime \prime}\left(\xi_{i}\right), \quad x_{i-1}<\xi_{i}<x_{i}, \quad i=1,2, \cdots, N-1 \\ y^{\prime}\left(x_{0}\right)=\frac{-3 y\left(x_{0}\right)+4 y\left(x_{1}\right)-y\left(x_{2}\right)}{2 h}+\frac{h^{2}}{3} y^{\prime \prime \prime}\left(\xi_{0}\right), \quad x_{0}<\xi_{0}<x_{2}, \\ y^{\prime}\left(x_{N}\right)=\frac{y\left(x_{N-2}\right)-4 y\left(x_{N-1}\right)+3 y\left(x_{N}\right)}{2 h}+\frac{h^{2}}{3} y^{\prime \prime \prime}\left(\xi_{N}\right), \quad x_{N-2}<\xi_{N}<x_{N} \end{array}\right. \] 略去误差，并用 \(y(x_i)\) 的近似值 \(y_i\) 代替 \(y(x_i)\), \(p_i=p(x_i),q_i=q(x_i),f_i=f(x_i)\) 便得到差分方程组 \[ \left\{\begin{array}{l} \frac{1}{h^{2}}\left(y_{i-1}-2 y_{i}+y_{i+1}\right)+\frac{p_{i}}{2 h}\left(y_{i+1}-y_{i-1}\right)+q_{1} y_{i}=f_{i}, \quad i=1,2, \cdots, N-1 \\ a_{1} y_{0}+\frac{a_{2}}{2 h}\left(-3 y_{0}+4 y_{1}-y_{2}\right)=\alpha \\ \beta_{1} y_{N}+\frac{\beta_{2}}{2 h}\left(y_{N-2}-4 y_{N-1}+3 y_{N}\right)=\beta \end{array}\right. \] 其中 \(q_{i}=q\left(x_{i}\right), p_{i}=p\left(x_{i}\right), f_{i}=f\left(x_{i}\right), i=1,2, \cdots, N-1, y_{i}\) 是 \(y\left(x_{i}\right)\) 的近似值. 整理得 \[\left\{\begin{array}{l}\left(2 h \alpha_{1}-3 \alpha_{2}\right) y_{0}+4 \alpha_{2} y_{1}-\alpha_{2} y_{2}=2 h \alpha \\ \left(2-h p_{i}\right) y_{i-1}-2\left(2-h^{2} q_{i}\right) y_{i}+\left(2+h p_{i}\right) y_{i+1}=2 h^{2} f_{i}, \quad i=1,2, \cdots, N-1 \\ \beta_{2} y_{N-2}-4 \beta_{2} y_{N-1}+\left(3 \beta_{2}+2 h \beta_{1}\right) y_{N}=2 h \beta\end{array}\right.\] 特别地, 若 \(\alpha_{1}=1, \alpha_{2}=0, \beta_{1}=1, \beta_{2}=0\), 则原问题中的边界条件是第一类边值条件: \(y(a)=\alpha, y(b)=\beta\); 此时方程组为 \[ \left\{\begin{array}{l} -2\left(2-h^{2} q_{1}\right) y_{1}+\left(2+h p_{1}\right) y_{2}=2 h^{2} f_{1}-\left(2-h p_{1}\right) \alpha, \\ \left(2-h p_{i}\right) y_{i-1}-2\left(2-h^{2} q_{1}\right) y_{i}+\left(2+h p_{i}\right) y_{i+1}=2 h^{2} f_{i}, \quad i=2,3, \cdots, N-2 \\ \left(2-h p_{N-1}\right) y_{N-2}-2\left(2-h^{2} q_{N-1}\right) y_{N-1}=2 h^{2} f_{N-1}-\left(2+h p_{N-1}\right) \beta \end{array}\right. \] 以上方程组是三对角方程组，用解三对角方程组的追赶法求解差分方程组，便得边值问题的差分解 . |
| 3. 讨论差分方程组的解是否收敛到原微分方程的解，估计误差. 这里就不再详细介绍. |
数值算例
考虑带有第三类边界条件的二阶常系数微分方程边值问题 \[ \left\{ \begin{aligned} y''(x)+2y'(x)-3y(x) & = 3x+1, & x\in [1,2]\\ y'(1)-y(1) & = 1,\\ y'(2)-y(2) & = -4. \end{aligned} \right. \] 1. 求出上述两点边值问题的解析解; 2. 通过有限差分方法算出其数值解;(取\(h=\frac{1}{5}\))并计算误差、绘图、输出\(1.0,1.2,1.4,1.6,1.8,2.0\)处的数值解.
问题二:有限差分方法算出其数值解及误差 对于原问题,取步长h=0.2,用有限差分求其近似解,并将结果与精确解y(x)=-x-1进行比较. >解:
因为 \[N=\frac{2-1}{h}=5,p(x)=2,q(x)=-3,f(x)=3x+1\] \[\alpha_1=-1,\alpha_2=1,\alpha=1\] \[\beta_1=1,\beta_2=1,\beta=-4\] >代入上述差分方程组公式得到差分格式 \[ \left\{\begin{array}{l} \left(-2h-3\right) y_{0}+4 y_{1}- y_{2}=2h \\ \left(2-2h\right) y_{i-1}-2\left(2+3h^{2} \right) y_{i}+\left(2+2h\right) y_{i+1}=2h^2f_i, \quad i=1,2, \cdots, N-1 \\ y_{N-2}-4 y_{N-1}+\left(3 + 2h\right) y_{N}=-8h\end{array}\right. \] 化简得 \[ \left\{\begin{array}{l} \left(-2h-3\right) y_{0}+4 y_{1}+(-1) y_{2}=2h \\ \left(2-2h\right) y_{i-1}+\left(-4-6h^{2} \right) y_{i}+\left(2+2h\right) y_{i+1}=2h^2f_i, \quad i=1,2, \cdots, N-1 \\ y_{N-2}+(-4) y_{N-1}+\left(3 + 2h\right) y_{N}=-8h\end{array}\right. \] 写成矩阵形式 \[\left[ \begin{matrix} -2h-3 & 4 & -1 & & & & \\ 2-2h & -4-6h^2 & 2+2h & & & & \\ & 2-2h & -4-6h^2 & 2+2h & & & \\ & & \ddots & \ddots & \ddots & & \\ & & & 2-2h & -4-6h^2 & 2+2h \\ & & & & 2-2h & -4-6h^2 & 2+2h \\ & & & & 1 & -4 & 3+2h \end{matrix} \right] \left[ \begin{matrix} y_0\\ y_1 \\ y_2 \\ \vdots \\ y_{N-2} \\ y_{N-1} \\ y_{N} \end{matrix} \right]=\left[ \begin{matrix} 2h \\ 2h^2f_1 \\ 2h^2f_2 \\ \vdots \\ 2h^2f_{N-2} \\ 2h^2f_{N-1} \\ -8h \end{matrix} \right]\] 令 \[A=\left[ \begin{matrix} -2h-3 & 4 & -1 & & & & \\ 2-2h & -4-6h^2 & 2+2h & & & & \\ & 2-2h & -4-6h^2 & 2+2h & & & \\ & & \ddots & \ddots & \ddots & & \\ & & & 2-2h & -4-6h^2 & 2+2h \\ & & & & 2-2h & -4-6h^2 & 2+2h \\ & & & & 1 & -4 & 3+2h \end{matrix} \right] , Y=\left[ \begin{matrix} y_0\\ y_1 \\ y_2 \\ \vdots \\ y_{N-2} \\ y_{N-1} \\ y_{N} \end{matrix}\right] , b=\left[ \begin{matrix} 2h \\ 2h^2f_1 \\ 2h^2f_2 \\ \vdots \\ 2h^2f_{N-2} \\ 2h^2f_{N-1} \\ -8h \end{matrix} \right]\] 得到代数方程 \[AY=b\] 使用解三对角方程组的追赶法求解此差分方程组,得到差分解 \(Y\).
二阶线性常系数微分方程边值问题的差分法
Python代码
先以将区间划分为5份为例，求出数值解 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48import numpy as np
import matplotlib.pyplot as plt
# 准备工作
def initial(L, R, NS):
x = np.linspace(L, R, NS + 1)
h = (R - L) / NS
return x, h
# 右端函数f
def f(x):
return 3 * x + 1
# 解方程
def solve(NS):
# 矩阵A
A1 = np.array([-2 * h - 3] + [b] * (NS - 1) + [3 + 2 * h])
# print("A1",A1)
A2 = np.array([a] * (NS - 1) + [-4])
# print("A2", A2)
A3 = np.array([4] + [c] * (NS - 1))
# print("A3", A3)
A4 = np.array([-1] + [0] * (NS - 2))
# print("A4", A4)
A5 = np.array([0] * (NS - 2) + [1])
# print("A5", A5)
A = np.diag(A1) + np.diag(A2, -1) + np.diag(A3, 1) + np.diag(A4, 2) + np.diag(A5, -2)
# print("A", A)
# 矩阵b
br = 2 * h ** 2 * f(x) + np.array(
[2 * h - 2 * h ** 2 * f(x[0])] + [0] * (NS - 1) + [-8 * h + 2 * h ** 2 * f(x[NS])])
uh = np.linalg.solve(A, br)
return uh
L = 1.0
R = 2.0
NS = 5
x, h = initial(L, R, NS)
a = 2 - 2 * h
b = -4 - 6 * h ** 2
c = 2 + 2 * h
uh = solve(NS)
print("h=%f时数值解\n" % h, uh)1
2h=0.200000时数值解
[-1.48151709 -1.56543883 -1.6245972 -1.6531625 -1.64418896 -1.58929215]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20# 真解函数
def ture_u(x):
ture_u = -x - 1
return ture_u
t_u = ture_u(x)
print("h=%f时真解\n" % h, t_u)
# 误差范数
def err(ture_u, uh):
ee = max(abs(ture_u - uh))
e0 = np.sqrt(sum((ture_u - uh) ** 2) * h)
return ee, e0
ee, e0 = err(t_u, uh)
print('L_∞(最大模)范数下的误差', ee)
print('L_2(平方和)范数下的误差', e0)1
2
3
4h=0.200000时真解
[-2. -2.2 -2.4 -2.6 -2.8 -3. ]
L_∞(最大模)范数下的误差 1.4107078471946164
L_2(平方和)范数下的误差 1.04835480203087841
2
3
4
5
6
7# 绘图比较
plt.figure()
plt.plot(x, uh, label='Numerical solution')
plt.plot(x, t_u, label='Exact solution')
plt.title("solution")
plt.legend()
plt.show()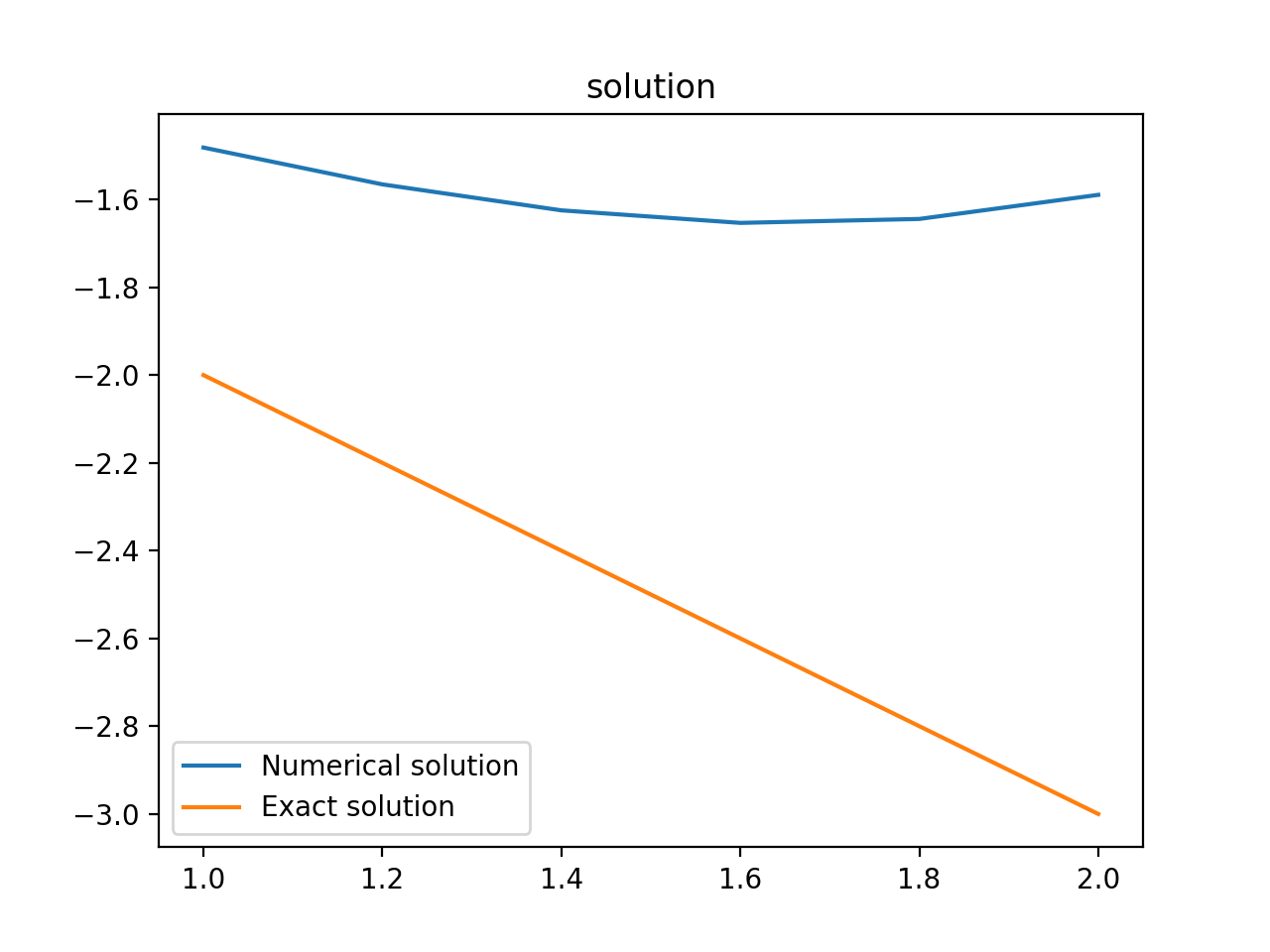
哎呀呀! 根据输出显示的误差,发现此时数值解的求解效果令人难以接受\(L_∞\)(最大模)范数下的误差高达1.41,从图像也能看出数值解与解析解不仅相差甚远,甚至连曲线走势都不太一致.(数值解为一条曲线,解析解为直线)
此处首先认为解析解或者查分格式计算错了,休息了一晚上起来重新推导了一遍后并未发现明显错误. 后来在玩GTA的时候忽然想起导师之前提到过步长会影响数值解稳定性···,于是重新编写程序,修改步长后发现确实如此.
将区间划分为 \(N=1280\) 份, 即 \(h=0.000781\) 时.
结果: 1
2
3
4
5
6
7
8h=0.000781时数值解
[-1.99798816 -1.99876784 -1.99954751 ... -2.99297729 -2.99375427
-2.99453125]
h=0.000781时真解
[-2. -2.00078125 -2.0015625 ... -2.9984375 -2.99921875
-3. ]
L_∞(最大模)范数下的误差 0.005468750663166322
L_2(平方和)范数下的误差 0.0035976563635910903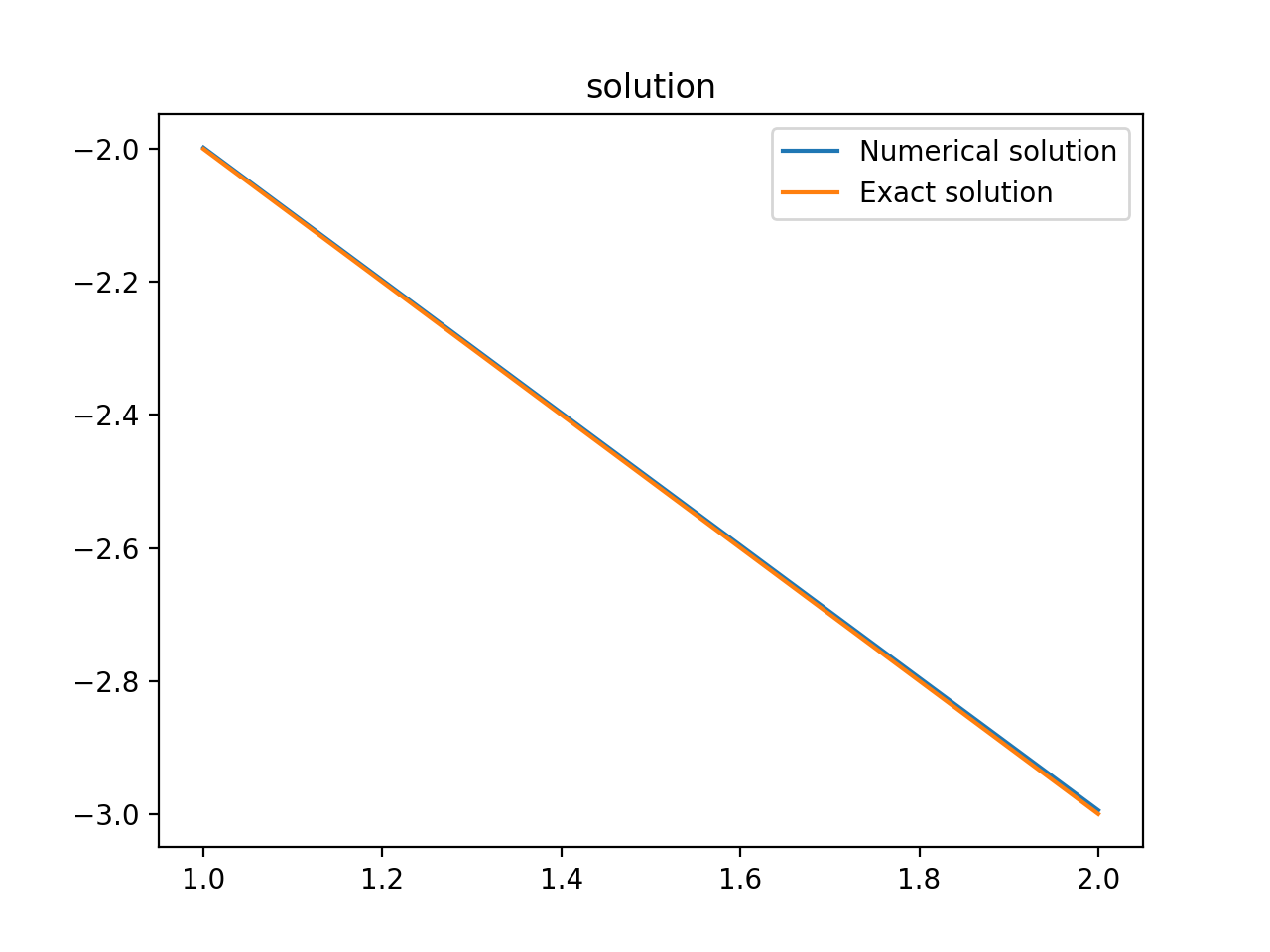
可以看到此时已经具有较高精度, 若还未达到需求精度, 可通过缩短步长\(h\) 继续提高精度.
最后，我们还可以从数学的角度分析所采用的差分格式的一些性质。因为差分格式的误差为\(O(h^2)\)， 所以理论上来说网格每加密一倍，与真解的误差大致会缩小到原来的\(\frac{1}{4}\). 下讨论网格加密时的变化： 1
2
3
4
5
6
7
8
9
10
11
12
13
14# 误差与网格关系讨论
N = [5, 10, 20, 40, 80, 160, 320, 640, 1280, 2560]
print("网格密度加倍时误差变化情况")
for i in range(len(N)):
NS = N[i]
x, h = initial(L, R, NS)
a = 2 - 2 * h
b = -4 - 6 * h ** 2
c = 2 + 2 * h
uh = solve(NS)
t_u = ture_u(x)
ee, e0 = err(t_u, uh)
print('步长h=%f' % h, end='\t')
print('最大模误差=%f' % ee)1
2
3
4
5
6
7
8
9
10
11网格密度加倍时误差变化情况
步长h=0.200000 最大模误差=1.410708
步长h=0.100000 最大模误差=0.701417
步长h=0.050000 最大模误差=0.350182
步长h=0.025000 最大模误差=0.175023
步长h=0.012500 最大模误差=0.087503
步长h=0.006250 最大模误差=0.043750
步长h=0.003125 最大模误差=0.021875
步长h=0.001563 最大模误差=0.010938
步长h=0.000781 最大模误差=0.005469
步长h=0.000391 最大模误差=0.002734
完整代码
1 | |
数值算例来源: 《微分方程数值解》-M.Ran
本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！