本文最后更新于：1 个月前

四川师范大学数学科学学院

2021 级研究生

《数值分析与科学计算》期末考试题

考生姓名: 刘洋

学号:20210801068

一、（30 分）误差是数值计算中一个非常重要的研究内容.请回答以下问题:

设 $I_{\mathrm{n}}=\int_{0}^{1} x^{n} e^{x-1} d x$, 求证:
1. $I_{\mathrm{n}}=1-n I_{n-1}, n=1,2,3, \ldots$ （5 分）
(2)正向递推时误差传播逐步放大, 逆向递推时误差传播逐步衰减.(15 分)

证：

$I_{n}=\int_{0}^{1} x^{n} e^{x-1} d x=\int_{0}^{1} x^{n} d e^{x-1}$ \[ =\left.x^{n} e^{x-1}\right|_{0} ^{1}-\int_{0}^{1} e^{x-1} \cdot n x^{n-1} d x=1-n I_{n-1} \]
正向递推时, 由 $I_{n-1}$ 来计算 $I_{n}$ : \[ I_{n}=1-n I_{n-1}, n=1,2,3, \cdots . \] 若已知 $I_{n-1}$ 的一个近似值 $\tilde{I}_{n-1}$, 则实际计算得到的 $I_{n}$ 的近似值 $\tilde{I}_{n}$ 为 \[ \tilde{I}_{n}=1-n \tilde{I}_{n-1}, n=1,2,3, \cdots \] 将以上两式相减得 \[ I_{n}-\tilde{I}_{n}=-n\left(I_{n-1}-\tilde{I}_{n-1}\right) \] 两边取绝对值得 \[ \left|I_{n}-\tilde{I}_{n}\right|=n\left|I_{n-1}-\tilde{I}_{n-1}\right| \text {. } \] 这说明 $I_{n-1}$ 的误差将放大 $\mathrm{n}$ 倍传到 $I_{n}$. 因而正向递推时误差传播逐步放大. 逆向递推时, 由 $I_{n}$ 来计算 $I_{n-1}$ : \[ I_{n-1}=\frac{1}{n}\left(1-I_{n}\right), n=N, N-1, N-1, \cdots, 2,1 . \] 若已知 $I_{n}$ 的一个近似值 $\tilde{I}_{n}$, 则实际计算得到的 $I_{n-1}$ 的近似值 $\tilde{I}_{n-1}$ 为 \[ \tilde{I}_{n-1}=\frac{1}{n}\left(1-\tilde{I}_{n}\right), n=N, N-1, N-1, \cdots, 2,1 . \] 将以上两式相减得 \[ I_{n-1}-\tilde{I}_{n-1}=-\frac{1}{n}\left(I_{n}-\tilde{I}_{n}\right) \] 两边取绝对值得 \[ \left|I_{n-1}-\tilde{I}_{n-1}\right|=\frac{1}{n}\left|I_{n}-\tilde{I}_{n}\right| \] 这说明 $I_{n}$ 的误差将缩小 $\mathrm{n}$ 倍传到 $I_{n-1}$. 逆向递推时误差传播逐步衰减.

在计算机上对 $1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}$ 自左向右求和: $S_{n}=\sum_{k=1}^{n} \frac{1}{k}$ .若 $n$ 很大, $S_{n}$ 将不随 $n$ 的增加而增加, 试说明原因.(10 分)

解

这主要是由于在计算机中作加法运算需先对位而造成的.例如, 设这台计算机具有 7 位精度, 即字长 $t=7$. 由 $S_{n}$ 的性质知, $S_{n}$ 单调增加且趋向于 $+\infty$, 另一方面通向项 $\frac{1}{n}$ 单调减少趋于零, 所以 $\frac{\frac{1}{m+1}}{S_{m}}$ 为单调减少序列.因而必存在 $m$ 使得 \[ \frac{\frac{1}{m+1}}{S_{m}}<\frac{1}{2} \times 10^{-7} \] 设 $S_{m}=0 \cdot a_{1} a_{2} \cdots a_{7} \times 10^{p}, a_{1} \neq 0$, 则

\[ \begin{aligned} &S_{m}+\frac{1}{m+1}=0 \cdot a_{1} a_{2} \cdots a_{7} \times 10^{p}+\frac{1}{m+1} \\ &=0 \cdot a_{1} a_{2} \cdots a_{7} \times 10^{p}+0.0000000 \times 10^{p} \\ &=\left(0 \cdot a_{1} a_{2} \cdots a_{7}+0.0000000 \times 10^{p}\right. \\ &=0 \cdot a_{1} a_{2} \cdots a_{7} \times 10^{p}=S_{m}, \end{aligned} \] \[ \text { 即 } S_{m+1}=S_{m} \text {. } \] 同理, 当 $k>m$ 时, \[ \begin{aligned} &S_{m}+\frac{1}{m+1}+\cdots+\frac{1}{k}=\left(S_{m}+\frac{1}{m+1}\right)+\cdots+\frac{1}{k} \\ &=\left(S_{m}+\frac{1}{m+2}\right)+\cdots+\frac{1}{k}=\cdots=S_{m}, \end{aligned} \] 即 \[S_{k}=S_{m} \]

二、（30 分）给定微分方程初值问题: \[ \left\{\begin{array}{l} y^{\prime}=\frac{2}{3} x y^{-2}, x \in[0,1.2] \\ y(0)=1 . \end{array}\right. \]

请用欧拉方法、改进的欧拉方法, 经典的龙格-库塔方法求解这个初值问题的数值解, 并将计算结果与准确值 $y=\sqrt[3]{1+x^{2}}$ 进行比较.数值结果要求步长分别取 $\mathrm{h}=0.4,0.2,0.1,0.05$ 列出数值解, 精确解, 绝对误差, 以及方法的收敛阶.(附程序)（20 分）

解答:

欧拉方法迭代公式: \[ y_{i+1}=y_{i}+h \cdot f\left(x_{i}, y_{i}\right), \quad(i=0,1,2, \cdots, n-1) \] 改进欧拉方法迭代公式: \[ y_{i+1}=y_{i}+\frac{h}{2}\left[f\left(x_{i}, y_{i}\right)+f\left(x_{i+1}, y_{i}+h f\left(x_{i}, y_{i}\right)\right)\right], \] 经典 R-K 方法迭代公式: \[ \left\{\begin{array}{l} y_{i+1}=y_{i}+\frac{h}{6} \cdot\left(K_{1}+2 K_{2}+2 K_{3}+K_{4}\right), \\ K_{1}=f\left(x_{i}, y_{i}\right), \\ K_{2}=f\left(x_{i}+\frac{h}{2}, y_{i}+\frac{h}{2} K_{1}\right), \\ K_{3}=f\left(x_{i}+\frac{h}{2}, y_{i}+\frac{h}{2} K_{2}\right), \\ K_{4}=f\left(x_{i}+h, y_{i}+h K_{3}\right) . \end{array}\right. \] >MATLAB程序代码 > >主程序 main.m

f_h=@ODE_fun;
%初值条件及求解区间
x0=0;
y0=1;
xn=1.20001;
%步长
h=0.1;
[~,Y1]=MethodClassicalRK(f_h,x0,y0,xn,h);
[~,Y2]=MethodImprovedEuler(f_h,x0,y0,xn,h);
[X,Y3]=MethodEuler(f_h,x0,y0,xn,h);
%精确解
Y=(1+X.*X).^(1/3);
plot(X,Y1,'kx',X,Y2,'go',X,Y3,'rx',X,Y,'b');
legend('经典R-K','改进欧拉方法','欧拉方法','精确解');
xlswrite('result.xlsx',[X;Y1;Y2;Y3;Y],1,'B1');

微分方程右端函数 ODE_fun.m

function result = ODE_fun( x, y )
%这是微分方程中的右端函数f
    result = 2/3*x/y/y;
end

欧拉法 MethodEuler.m

function [ X,Y ] = MethodEuler(f_h,x0,y0,xn,h )
%用欧拉法求解微分方程
    n=floor((xn-x0)/h);
    X=zeros(1,n+1);
    Y=zeros(1,n+1);
    X(1)=x0;
    Y(1)=y0;
    for i=2:(n+1)
       X(i)=X(i-1)+h;
       Y(i)=Y(i-1)+h*feval(f_h,X(i-1),Y(i-1));
    end
end

改进的欧拉法 MethodImprovedEuler.m

function [ X,Y ] = MethodImprovedEuler(f_h,x0,y0,xn,h )
%使用改进的欧拉法求解微分方程
    n=floor((xn-x0)/h);
    X=zeros(1,n+1);
    Y=zeros(1,n+1);
    X(1)=x0;
    Y(1)=y0;
    for i=2:(n+1)
       X(i)=X(i-1)+h;
       Y(i)=Y(i-1)+h/2*(feval(f_h,X(i-1),Y(i-1))+feval(f_h,X(i),Y(i-1)+h*feval(f_h,X(i-1),Y(i-1))));
    end
end

经典的 r-k 方法 MethodClassicalRK.m

 function [ X,Y ] = MethodClassicalRK(f_h,x0,y0,xn,h )
%用经典的 r-k 方法求解微分方程
    n=floor((xn-x0)/h);
    X=zeros(1,n+1);
    Y=zeros(1,n+1);
    X(1)=x0;
    Y(1)=y0;
    for i=2:(n+1)
       X(i)=X(i-1)+h;
       k1=feval(f_h,X(i-1),Y(i-1));
       k2=feval(f_h,X(i-1)+h/2,Y(i-1)+h/2*k1);
       k3=feval(f_h,X(i-1)+h/2,Y(i-1)+h/2*k2);
       k4=feval(f_h,X(i-1)+h,Y(i-1)+h*k3);
       Y(i)=Y(i-1)+h/6*(k1+2*k2+2*k3+k4);
    end
end

程序运行结果:

$h=0.4$

对比图像

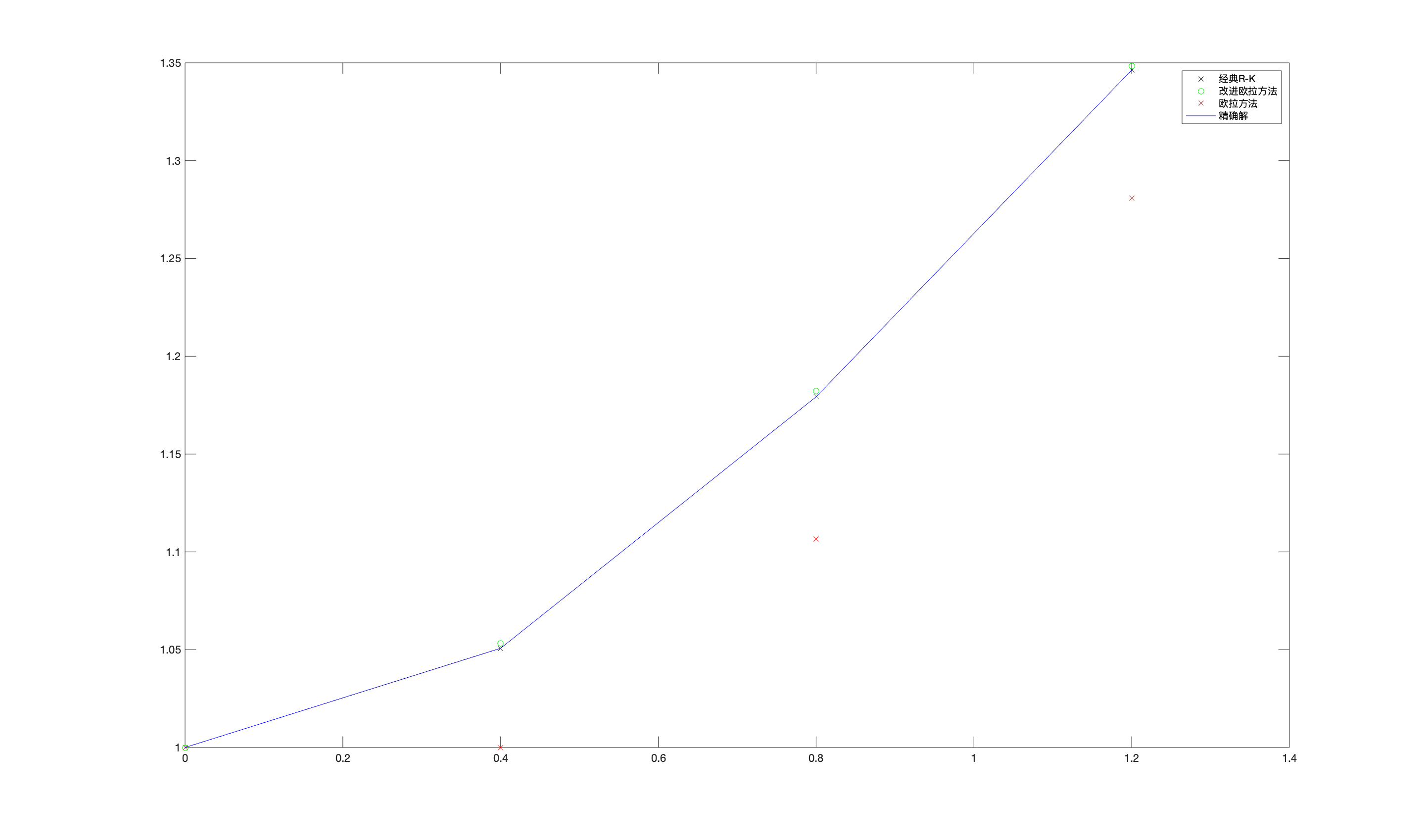0.4 >数值结果:

x	0.4	0.8	1.2
精确解	1.0507	1.1793	1.3463
经典R-K数值解	1.0508	1.1793	1.3463
经典R-K误差	3.3048e-05	5.8051e-05	5.2326e-05
改进欧拉数值解	1.0533	1.1821	1.3483
改进欧拉误差	0.0026158	0.0028583	0.0020025
欧拉数值解	1	1.1067	1.2809
欧拉误差	0.050718	0.072607	0.065406

$h=0.2$

对比图像

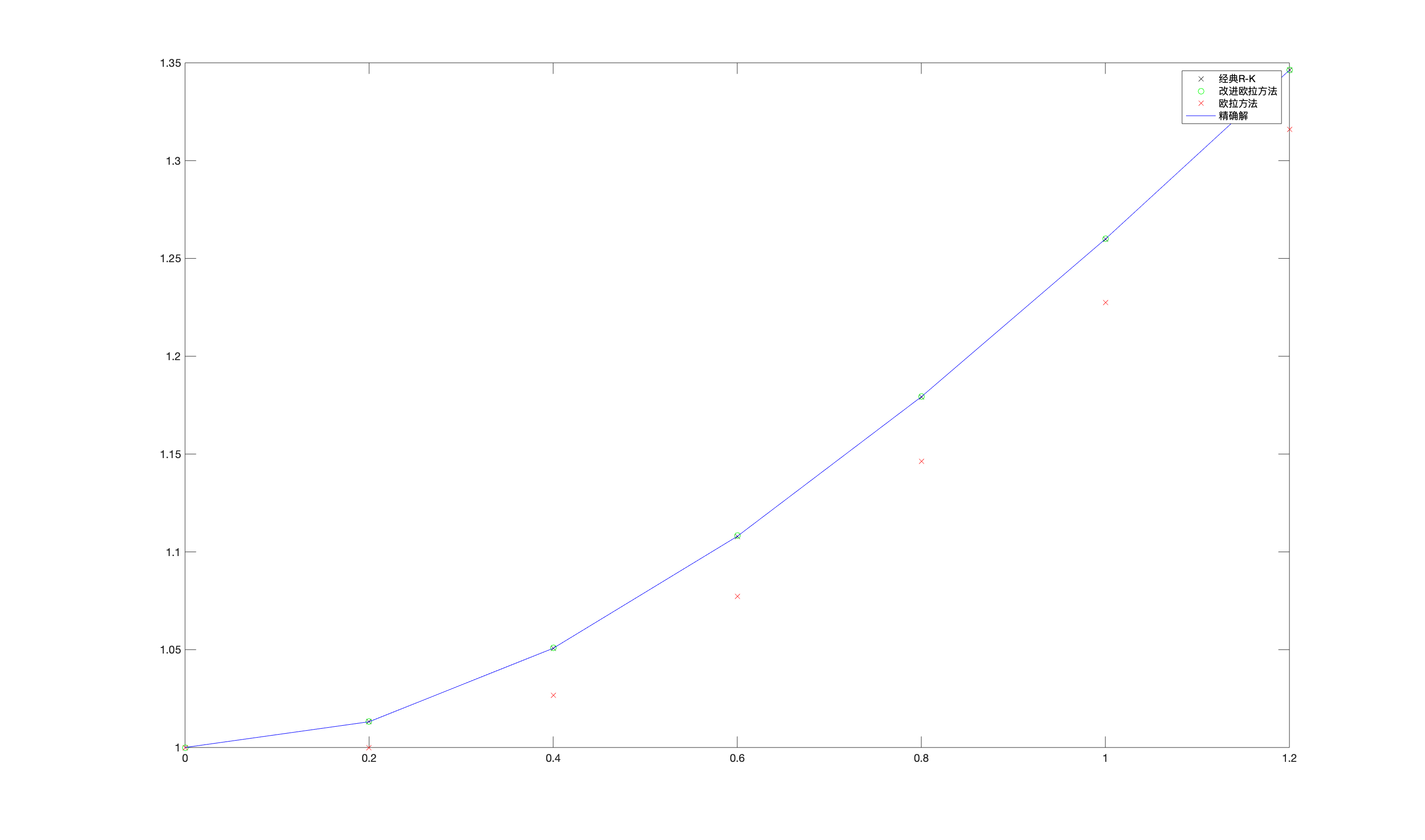0.2 >数值结果:

x	0.2	0.4	0.6	0.8	1	1.2
精确解	1.0132	1.0507	1.1079	1.1793	1.2599	1.3463
经典R-K数值解	1.0132	1.0507	1.1079	1.1793	1.2599	1.3463
经典R-K误差	5.7205e-07	1.7831e-06	2.7101e-06	3.0503e-06	2.9862e-06	2.7464e-06
改进欧拉数值解	1.0133	1.051	1.1082	1.1796	1.2601	1.3464
改进欧拉误差	0.00017393	0.00028844	0.0003162	0.00027816	0.00020853	0.00013214
欧拉数值解	1	1.0267	1.0773	1.1462	1.2274	1.3159
欧拉误差	0.013159	0.024051	0.030666	0.033073	0.032529	0.030365

$h=0.1$

对比图像

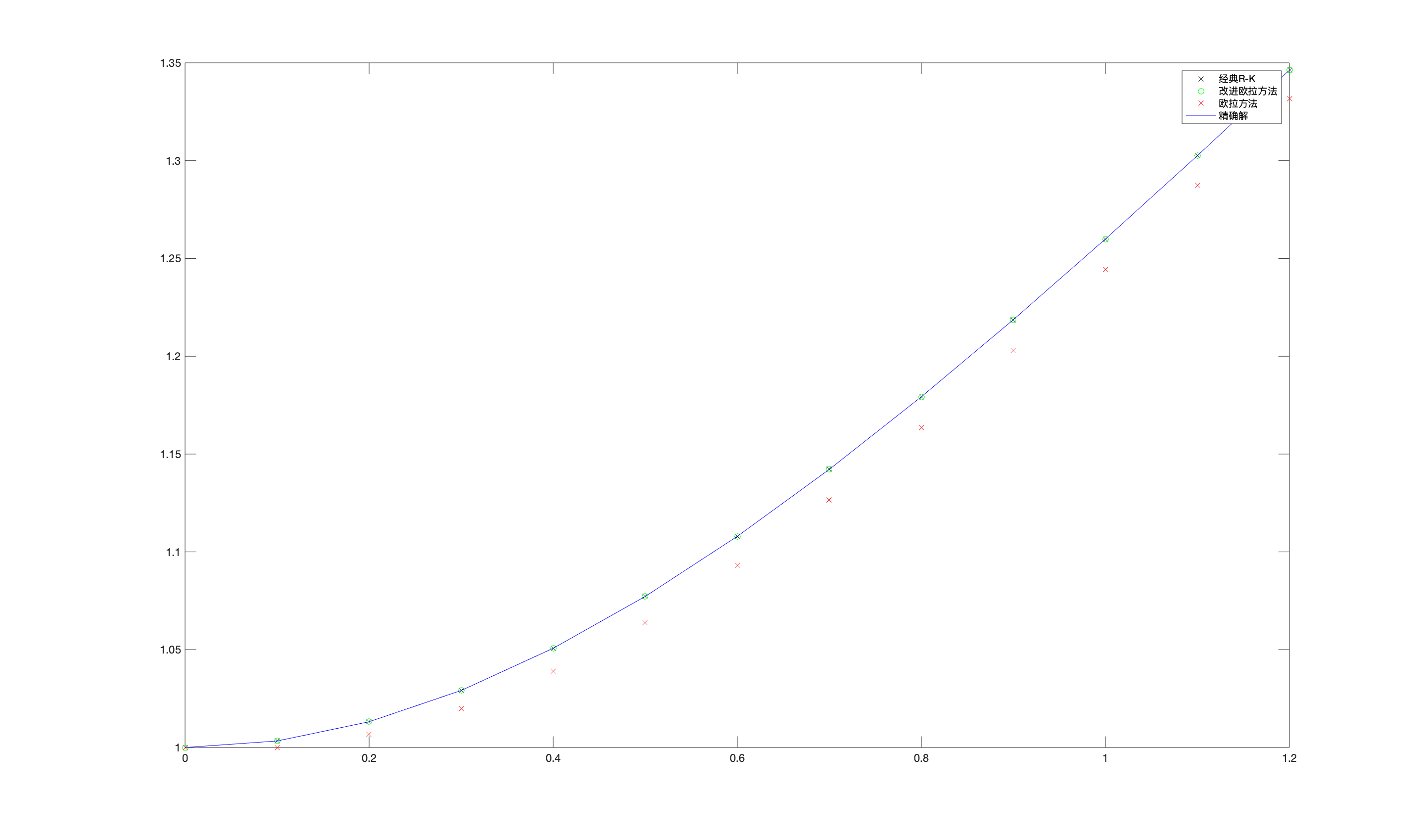0.1 >数值结果:

x	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1	1.1	1.2
精确解	1.0033	1.0132	1.0291	1.0507	1.0772	1.1079	1.1422	1.1793	1.2187	1.2599	1.3026	1.3463
经典R-K数值解	1.0033	1.0132	1.0291	1.0507	1.0772	1.1079	1.1422	1.1793	1.2187	1.2599	1.3026	1.3463
经典R-K误差	9.1775e-09	3.4381e-08	6.8868e-08	1.0452e-07	1.3498e-07	1.5702e-07	1.702e-07	1.7579e-07	1.7567e-07	1.7169e-07	1.6534e-07	1.5773e-07
改进欧拉数值解	1.0033	1.0132	1.0292	1.0508	1.0773	1.108	1.1422	1.1793	1.2187	1.2599	1.3026	1.3463
改进欧拉误差	1.105e-05	2.1031e-05	2.8778e-05	3.3505e-05	3.4966e-05	3.3402e-05	2.9377e-05	2.3576e-05	1.6668e-05	9.216e-06	1.6546e-06	5.709e-06
欧拉数值解	1	1.0067	1.0198	1.0391	1.0638	1.0932	1.1267	1.1634	1.2028	1.2443	1.2874	1.3316
欧拉误差	0.0033223	0.0064927	0.0093185	0.011664	0.013464	0.01472	0.015484	0.01583	0.015844	0.015607	0.015187	0.014643

$h=0.05$

对比图像

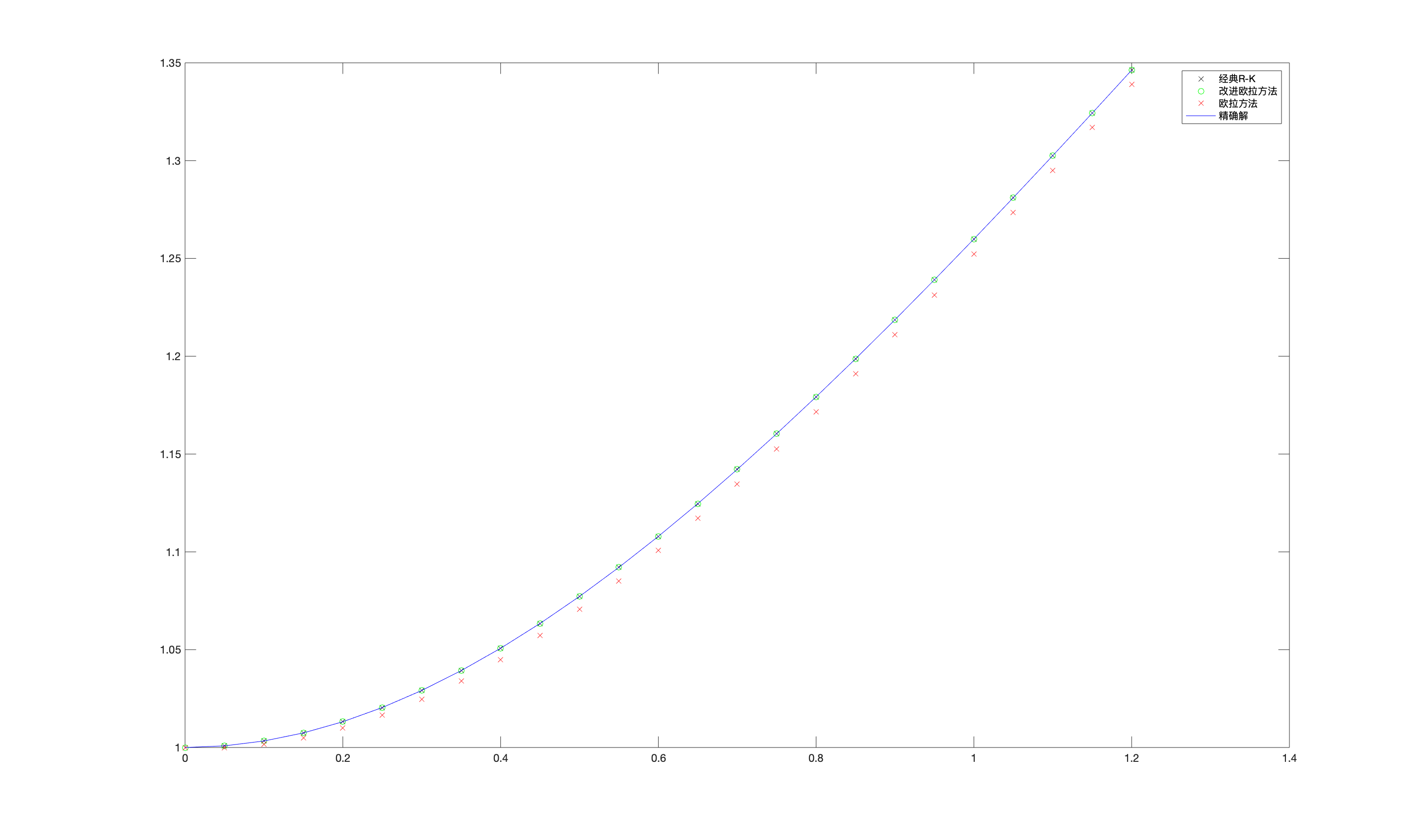0.05 >数值结果:

x	0.05	0.1	0.15	0.2	0.25	0.3	0.35	0.4	0.45	0.5	0.55	0.6	0.65	0.7	0.75	0.8	0.85	0.9	0.95	1	1.05	1.1	1.15	1.2
精确解	1.0008	1.0033	1.0074	1.0132	1.0204	1.0291	1.0393	1.0507	1.0634	1.0772	1.0921	1.1079	1.1247	1.1422	1.1604	1.1793	1.1987	1.2187	1.2391	1.2599	1.2811	1.3026	1.3243	1.3463
经典R-K数值解	1.0008	1.0033	1.0074	1.0132	1.0204	1.0291	1.0393	1.0507	1.0634	1.0772	1.0921	1.1079	1.1247	1.1422	1.1604	1.1793	1.1987	1.2187	1.2391	1.2599	1.2811	1.3026	1.3243	1.3463
经典R-K误差	1.4435e-10	5.6792e-10	1.2396e-09	2.11e-09	3.1187e-09	4.2006e-09	5.2938e-09	6.3446e-09	7.3109e-09	8.1634e-09	8.8852e-09	9.4701e-09	9.9205e-09	1.0245e-08	1.0455e-08	1.0567e-08	1.0593e-08	1.0549e-08	1.0449e-08	1.0303e-08	1.0123e-08	9.9176e-09	9.6938e-09	9.4577e-09
改进欧拉数值解	1.0008	1.0033	1.0074	1.0132	1.0204	1.0291	1.0393	1.0507	1.0634	1.0772	1.0921	1.1079	1.1247	1.1422	1.1604	1.1793	1.1987	1.2187	1.2391	1.2599	1.2811	1.3026	1.3243	1.3463
改进欧拉误差	6.9348e-07	1.3696e-06	2.0058e-06	2.5782e-06	3.064e-06	3.4433e-06	3.7008e-06	3.8264e-06	3.8159e-06	3.6708e-06	3.397e-06	3.0047e-06	2.5066e-06	1.9173e-06	1.2522e-06	5.2662e-07	2.4462e-07	1.0478e-06	1.8704e-06	2.7015e-06	3.5317e-06	4.3529e-06	5.1585e-06	5.9432e-06
欧拉数值解	1	1.0017	1.005	1.0099	1.0165	1.0245	1.0341	1.045	1.0572	1.0706	1.0852	1.1007	1.1172	1.1346	1.1527	1.1715	1.191	1.2109	1.2314	1.2523	1.2735	1.2951	1.317	1.3391
欧拉误差	0.00083264	0.0016556	0.0024555	0.00322	0.0039383	0.0046016	0.0052034	0.0057394	0.0062076	0.0066079	0.0069419	0.0072124	0.0074235	0.0075798	0.0076862	0.0077479	0.0077701	0.0077576	0.0077151	0.0076469	0.0075571	0.0074491	0.0073262	0.0071911

结果分析:

可以看出，在 $h$ 取 0.1 的情况下，经典 R-K 方法计算出的结果有 7 位有效数字，改进欧拉方法计算出的结果有 5 位有效数字，欧拉方法计算出的结果有 2 位有效数字。

通过理论分析已知,欧拉方法总体收敛阶为 1 阶, 改进欧拉方法总体收敛阶为 2 阶, 经典 R-K 方法总体收敛阶为 4 阶.(这点从数值结果的误差也能验证出来,此处不再赘述)

证明下列求解公式是一个 3 阶方法.(10 分) \[ \left\{\begin{array}{l} y_{i+1}=y_{i}+\frac{h}{4}\left(k_{1}+3 k_{3}\right) \\ k_{1}=f\left(x_{i}, y_{i}\right) \\ k_{2}=f\left(x_{i}+\frac{h}{3}, y_{i}+\frac{h}{3} k_{1}\right) \\ k_{3}=f\left(x_{i}+\frac{2 h}{3}, y_{i}+\frac{2 h}{3} k_{2}\right) \end{array}\right. \]

解答

三阶 R-K 公式如下: \[y_{n+1}=y_{n}+\sum_{i=1}^{r} \omega_{i} k_{i} \] 其中: \[ \begin{aligned} &k_{1}=h f\left(x_{n}, y_{n}\right)=h f_n \\ &k_{2}=h f\left(x_{n}+a_{2} h, y_{n}+b_{21} k_{1}\right) \\ &k_{3}=h f\left(x_{n}+a_{3} h, y_{n}+b_{31} k_{1}+b_{32} k_{2}\right) \end{aligned} \]

将 $k_{2}$ 按二元函数在 $\left(x_n, y_n\right)$ 处按 Taylor 公式展开, $\quad\left(f_{n}=f\left(x_{n}, y_{n}\right)\right)$

\[ f\left(x_{n}+a_{2}h, y_{n}+b_{21} k_{1}\right)=f_{n}+a_{2} h f_{x}+b_{21} h f_{n} f_{y}+\frac{1}{2}\left(a_{2}^{2} h^{2} f_{x x}+\right. \left.2 a_{2} h^{2} b_{21} f_{n} f_{x y}+b_{21}^{2} h^{2} f_{n}^{2} f_{y y}\right)+O\left(h^{3}\right) \]

然后 $k_{3}$ 作类似的处理(注意: 将其中的 $k_{2}$ 用上式代替, 并注意略去导致最终展开式中的 $O\left(h^{4}\right)$ 项) \[ \begin{aligned} &f\left(x_{n}+a_{3} h, y_{n}+b_{31} h f_{n}+b_{32} k_{2}\right)=f_{n}+a_{3} h f_{x}+b_{31} h f_{n} f_{y}+ \\ &+b_{32} h\left(f_{n}+a_{2} h f_{x}\right) f_{y}+b_{32} b_{21} h^{2} f_{n} f_{y} f_{y}+\frac{1}{2}\left(a_{3}^{2} h^{2} f_{x}+\right. \\ &\left.\left.2 a_{3} h^{2} b_{31} f_{n} f_{x y}+2 a_{3} h^{2} b_{32} f_{n}\right)+\left(b_{31}^{2}+b_{32}^{2}\right) h^{2} f_{n}^{2} f_{y y}+2 b_{31} b_{32}\right) h^{2} f_{n}^{2} f_{y y}+O\left(h^{3}\right) \end{aligned} \]

将上述公式带入总公式即可.

然后再与 $y\left(x_{n+1}\right)$ 在点 $x_{n}$ 处的泰勒展开式 (如下) 比较 \[ \begin{aligned} &y_{(x _{n+1})}=y_{\left(x_{n}\right)}+h y^{\prime} +\frac{h^{2}}{2} y^{\prime\prime}+\frac{h^{3}}{6} y^{\prime\prime\prime}+O\left(h^{4}\right) \\ &=y_{n}+h f_n+\frac{1}{2}\left(f_{x}+f_{y} f\right) h^{2}+\frac{1}{6}\left(f_{x x}+2 f_{x y} f\right. \\ &\left.+f_{y} f_{x}+f_{y y} f^{2}+f_{y} f_{y} f\right) h^{3}+O\left(h^{4}\right) \end{aligned} \] 使对应项的系数相等, 简单分析即可得到: \[ \begin{aligned} &\omega_{1}+\omega_{2}+\omega_{3}=1 \\ &a_{2}=b_{21} \\ &a_{3}=b_{31}+b_{32} \\ &\omega_{2} a_{2}+\omega_{3} a_{3}=\frac{1}{2} \\ &\omega_{2} a_{2}^{2}+\omega_{3} a_{3}^{2}=\frac{1}{3} \\ &\omega_{3} b_{32} a_{2}=\frac{1}{6} \end{aligned} \]

这是 8 个未知数 6 个方程的方程组,解存在且解不唯一.

注意到原问题中对应系数分别为

\[ \begin{aligned} &\omega_{1}=\frac{1}{4},\ \omega_{2}=0,\ \omega_{3}=\frac{3}{4} \\ &a_{2}=b_{21}=\frac{1}{3} \\ &a_{3}=b_{32}=\frac{2}{3} \\ &b_{31}=0 \end{aligned} \]

容易验证,上述系数满足方程组,故证得该求解公式是一个 3 阶方法.

参考资料: 同济大学计算数学教研室.《数值分析基础》.同济大学出版社

三、(10 分) 对于方程组 \[ \left(\begin{array}{cccccc} a_{1} & c_{1} & & & & \\ b_{2} & a_{2} & c_{2} & & & \\ & b_{3} & a_{3} & & & \\ & & & \ddots & & \\ & & & & a_{n-1} & c_{n-1} \\ v_{1} & v_{2} & v_{3} & \cdots & v_{n-1} & v_{n} \end{array}\right)\left(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \\ x_{n-1} \\ x_{n} \end{array}\right)=\left(\begin{array}{c} d_{1} \\ d_{2} \\ d_{3} \\ d_{n-1} \\ d_{n} \end{array}\right) \] 给出一个追赶法设计方案, 并估算运算次数（乘除次数+加减次数).

解答

追赶法是求解三对角型线性方程组的一类常用方法，因其计算公式简单，运算量和存储量小，近年来被先后推广应用于循环三对角、五对角、反五对角与拟反五对角线性方程组、七对角线性方程组等对角型线性方程组.

显然题中给出矩阵为箭形矩阵,下面利用矩阵分解，结合箭形矩阵的结构特点，构建更加一般的箭形线性方程组的追赶法.

预备知识

定义 1 称如下结构的 $n$ 阶实矩阵为箭形矩阵: \[ A=\left(\begin{array}{ccccccc} a_{1} & f_{2} & f_{3} & f_{4} & \cdots & f_{n-1} & f_{n} \\ e_{2} & a_{2} & c_{2} & & & & \\ e_{3} & b_{3} & a_{3} & c_{3} & & & \\ e_{4} & & b_{4} & a_{4} & c_{4} & & \\ \vdots & & & \ddots & \ddots & \ddots & \\ e_{n-1} & & & & b_{n-1} & a_{n-1} & c_{n-1} \\ e_{n} & & & & & b_{n} & a_{n} \end{array}\right) . \]

本文假设箭形矩阵 $A$ 满足如下条件 $(*)$ : \[(1)\ b_{i} \neq 0(i=3,4, \cdots, n), c_{i} \neq 0(i=2,3, \cdots, n), e_{i}, f_{i} \neq 0(i=2,3, \cdots, n).\]

\[(2)\ \left|a_{1}\right|>\sum_{i=2}^{n}\left|f_{i}\right|,\left|a_{2}\right|>\left|e_{2}\right|+\left|c_{2}\right|,\left|a_{i}\right|>\left|b_{i}\right|+\left|c_{i}\right|+\left|e_{i}\right|,\left|a_{n}\right|>\left|e_{n}\right|+\left|b_{n}\right|.\]

引理 $1$ 若矩阵 $A=\left(a_{i j}\right) \in R^{n \times n}$ 严格对角占优, 则 $a_{i i} \neq 0$ 且 $A$ 为非奇异矩阵.

引理 $2$ 设矩阵 $A \in \mathbb{R}^{n \times n}$ 的各阶顺序主子式不等于零, 则存在唯一的分解 $A=M N$, 其中 $M$ 为上三角矩阵, $N$ 为单位下三角矩阵.

推论 $1$ 若箭形矩阵 $A$ 满足条件 $(*)$, 则 $A$ 非奇异且存在唯一的分解 $A=M N$, 其中 $M$ 为上三角矩阵, $N$ 为单位下三角矩阵.

证明若箭形矩阵 $A$ 满足条件 $(*)$, 则其各阶顺序主子阵仍满足条件 $(*)$. 根据引理 1 和引理 2, $A$ 为非奇异矩阵, 且 $A$ 的各阶顺序主子式均不等于零. 从而存在唯一的分解 $A=M N$, 其中 $M$ 为上三角矩阵, $N$ 为单位下三角矩阵.

箭形线性方程组的追赶法

考虑如下箭形线性代数方程组: \[ \left(\begin{array}{ccccccc} a_{1} & f_{2} & f_{3} & f_{4} & \cdots & f_{n-1} & f_{n} \\ e_{2} & a_{2} & c_{2} & & & & \\ e_{3} & b_{3} & a_{3} & c_{3} & & & \\ e_{4} & & b_{4} & a_{4} & c_{4} & & \\ \vdots & & & \ddots & \ddots & \ddots & \\ e_{n-1} & & & & b_{n-1} & a_{n-1} & c_{n-1} \\ e_{n} & & & & & b_{n} & a_{n} \end{array}\right)\left(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \\ \vdots \\ x_{n-1} \\ x_{n} \end{array}\right)=\left(\begin{array}{c} d_{1} \\ d_{2} \\ d_{3} \\ d_{4} \\ \vdots \\ d_{n-1} \\ d_{n} \end{array}\right) . \] 简记为: $A x=d$. 假设箭形矩阵 $A$ 满足条件 $(*)$, 根据推论 1 , 可实现矩阵分解 $A=M N$. 分解形式为: \[ A=\left(\begin{array}{ccccccc} l_{1} & r_{2} & r_{3} & r_{4} & \cdots & r_{n-1} & r_{n} \\ & l_{2} & m_{2} & & & & \\ & & l_{3} & m_{3} & & & \\ & & & l_{4} & m_{4} & & \\ & & & \ddots & \ddots & \ddots & \\ & & & & & l_{n-1} & m_{n-1} \\ & & & & & & l_{n} \end{array}\right)\left(\begin{array}{ccccccc} 1 & & & & & & \\ t_{2} & 1 & & & & & \\ t_{3} & s_{3} & 1 & & & & \\ t_{4} & & s_{4} & 1 & & & \\ \vdots & & & \ddots & \ddots & & \\ t_{n-1} & & & & s_{n-1} & 1 & \\ t_{n} & & & & & s_{n} & 1 \end{array}\right)=M N . \] 利用矩阵乘法, \[ A=\left(\begin{array}{ccccccc} l_{1}+\sum_{i=2}^{n} r_{i} t_{i} & r_{2}+r_{3} s_{3} & r_{3}+r_{4} s_{4} & r_{4}+r_{5} s_{5} & \cdots & r_{n-1}+r_{n} s_{n} & r_{n} \\ l_{2} t_{2}+m_{2} t_{3} & l_{2}+m_{2} s_{3} & m_{2} & & & & \\ l_{3} t_{3}+m_{3} t_{4} & l_{3} s_{3} & l_{3}+m_{3} s_{4} & m_{3} & & & \\ l_{4} t_{4}+m_{4} t_{5} & & l_{4} s_{4} & l_{4}+m_{4} s_{5} & m_{4} & & \\ & & & \ddots & \ddots & \ddots & \\ l_{n-1} t_{n-1}+m_{n-1} t_{n} & & & & l_{n-1} s_{n-1} & l_{n-1}+m_{n-1} s_{n} & m_{n-1} \\ l_{n} t_{n} & & & & & l_{n} s_{n} & l_{n} \end{array}\right) . \] 比较上式两边元素, 可得: \[ \left\{\begin{array}{l} l_{n}=a_{n}, r_{n}=f_{n}, s_{n}=b_{n} / a_{n}, t_{n}=e_{n} / a_{n}, \\ m_{i}=c_{i}, l_{i}=a_{i}-c_{i} s_{i+1}, s_{i}=b_{i} / l_{i}(i=n-1, n-2, \cdots, 2), \\ t_{i}=\left(e_{i}-c_{i} t_{i+1}\right) / l_{i}, r_{i}=f_{i}-r_{i+1} s_{i+1}(i=n-1, n-2, \cdots, 2), \\ l_{1}=a_{1}-\sum_{i=2}^{n} r_{i} t_{i} . \end{array}\right. \]

从而可将求解方程组 $A x=f$ 化为依次求解 $\left\{\begin{array}{l}M y=d, \\ U x=y .\end{array}\right.$ 具体算法如下:

第一步: 获得 $A$ 的三角分解 $A=M N$, 元素计算公式为上式. 第二步: 解方程组 $M y=d$, 即“追” 的过程. 解方程组: \[ \left(\begin{array}{ccccccc} l_{1} & r_{2} & r_{3} & r_{4} & \cdots & r_{n-1} & r_{n} \\ & l_{2} & m_{2} & & & & \\ & & l_{3} & m_{3} & & & \\ & & & l_{4} & m_{4} & & \\ & & & \ddots & \ddots & \ddots & \\ & & & & & l_{n-1} & m_{n-1} \\ & & & & & & l_{n} \end{array}\right)\left(\begin{array}{c} y_{1} \\ y_{2} \\ y_{3} \\ y_{4} \\ \vdots \\ y_{n-1} \\ y_{n} \end{array}\right)=\left(\begin{array}{c} d_{1} \\ d_{2} \\ d_{3} \\ d_{4} \\ \vdots \\ d_{n-1} \\ d_{n} \end{array}\right) . \] 得其解为: \[ \left\{\begin{array}{l} y_{n}=d_{n} / l_{n}, \\ y_{i}=\left(d_{i}-m_{i} y_{i+1}\right) / l_{i}(i=n-1, n-2, \cdots, 2), \\ y_{1}=\left(d_{1}-\sum_{i=2}^{n} r_{i} y_{i}\right) / l_{1} . \end{array}\right. \] 第三步: 解方程组 $N x=y$, 即“赶” 的过程. 解方程组: \[ \left(\begin{array}{ccccccc} 1 & & & & & & \\ t_{2} & 1 & & & & & \\ t_{3} & s_{3} & 1 & & & & \\ t_{4} & & s_{4} & 1 & & & \\ \vdots & & & \ddots & \ddots & & \\ t_{n-1} & & & & s_{n-1} & 1 & \\ t_{n} & & & & & s_{n} & 1 \end{array}\right)\left(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \\ \vdots \\ x_{n-1} \\ x_{n} \end{array}\right)=\left(\begin{array}{c} y_{1} \\ y_{2} \\ y_{3} \\ y_{4} \\ \vdots \\ y_{n-1} \\ y_{n} \end{array}\right) . \] 得其解为: \[ \left\{\begin{array}{l} x_{1}=y_{1}, \\ x_{2}=y_{2}-t_{2} x_{1}, \\ x_{i+1}=y_{i+1}-t_{i+1} x_{1}-s_{i+1} x_{i}(i=2,3, \cdots, n-1) . \end{array}\right. \]

运算量分析

上述算法即为求解箭形线性方程组的追赶法. 用追赶法求解 $n$ 阶箭形线性方程组, 矩阵分解, “追” 和 “赶” 的过程分别需要 $6 n-10 、 3 n-3 、 2 n-3$ 次乘、除法, 合计只需 $(11 n-16)$ 次乘除法, 而大家熟知的高斯消元法的运算量是 $\left(n^{3} / 3+n^{2}-n / 3\right)$. 由此可见, 当 $n$ 较大时, 追赶法的运算量比高斯消元法少很多.

参考文献:

叶志翔,蔡静.求解箭形线性方程组的一类追赶法[J].湖州师范学院学报,2019,41(02):11-15.

四、（20 分）迭代法是求解非线性方程 $f(x)=0$ 最常用的数值方法, 请回答

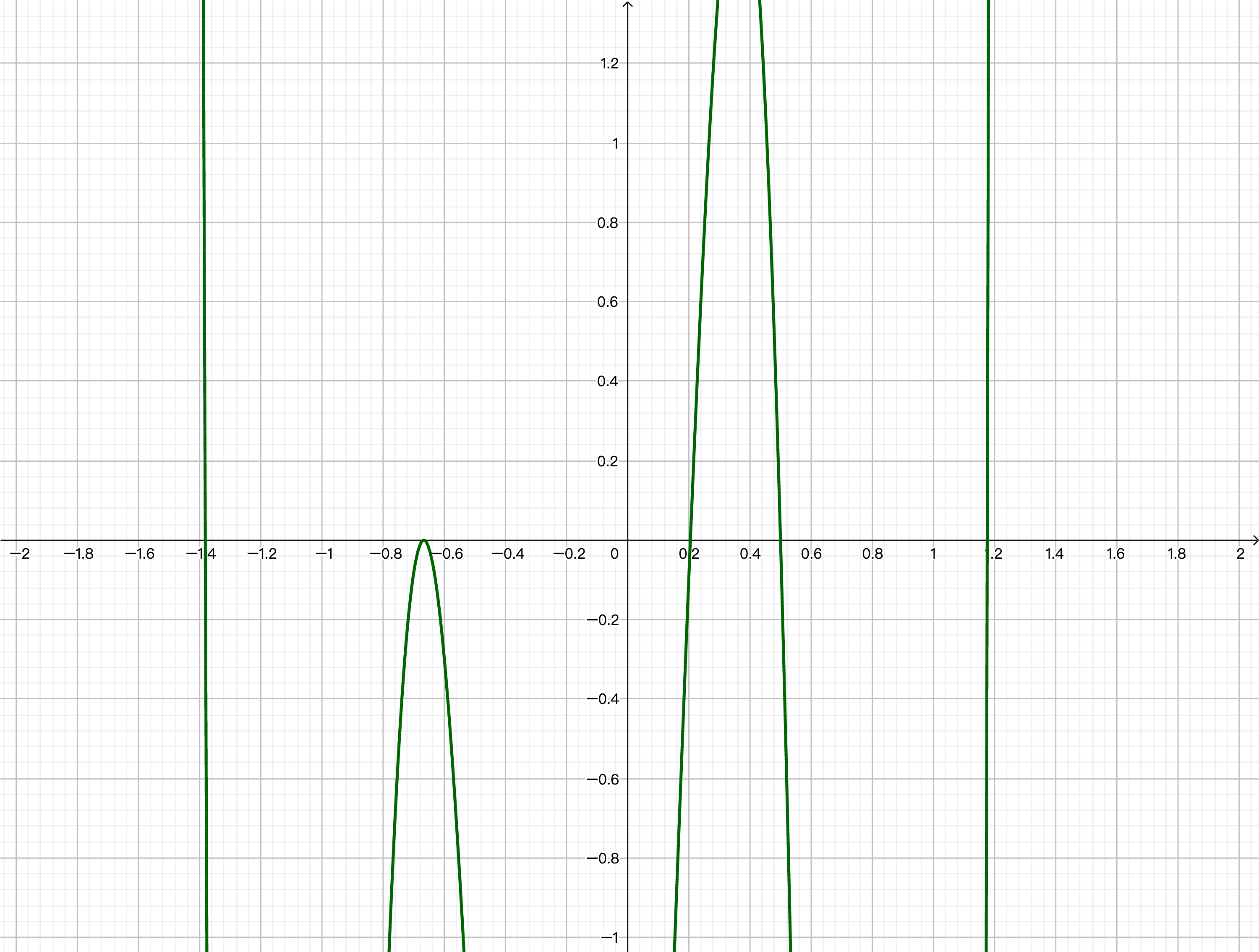
设 $f(x)=54 x^{6}+45 x^{5}-102 x^{4}-69 x^{3}+35 x^{2}+16 x-4$, 画出函数在 $[-2,2]$ 上的函数图形, 并用 $Newton$ 迭代法求这个区间内方程 $f(x)=0$ 的 5 个根, 给出数值算例的结果, 观察取不同初值时 $Newton$ 迭代法的收敛情况, 并分析计算结果.（10 分）

解答

函数整体图形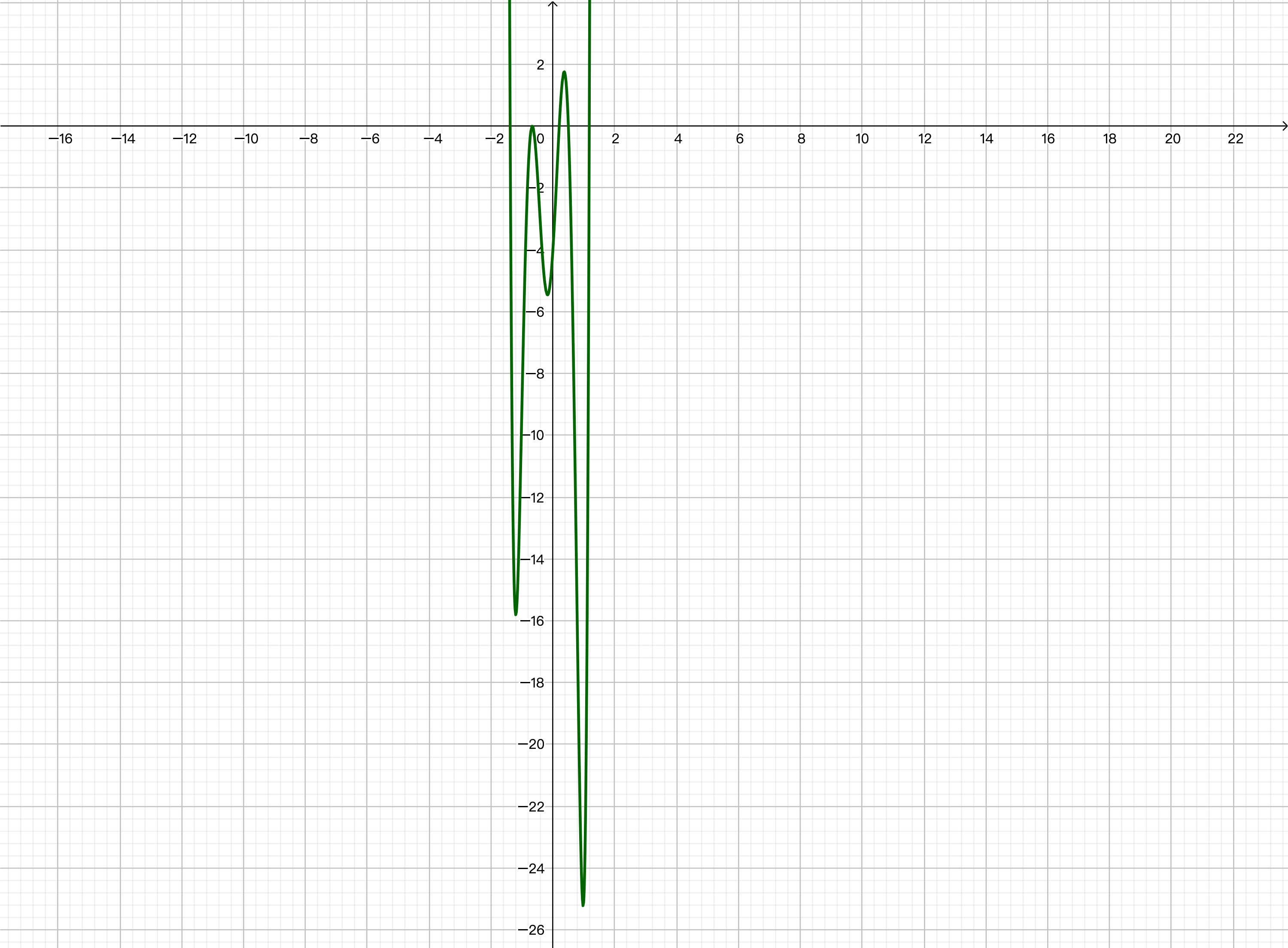

函数在 $[-2,2]$ 上的函数图形

通过使用张莉老师在数值分析与算法课程上提出的二方法求根的改进方法,估计出方程的根的个数及其所在区间,为启动Newton迭代的初值选择做准备.

具体步骤:

Step1: 对求解区间$[a,b]$做网格剖分,取正整数$n$.将$[a,b]$作$n$等分.记$h=\frac{b-a}{n};x_i=ih,0\le i\le n$.
Step2: 从第一个子区间$[x_i,x_{i+1}],i=0$,开始判定
- 是否满足:$f(x_i)=0\ 或者\ f(x_{i+1})=0$
  - 是:得到$x_i\ 或\ x_{i+1}$作为近似根$x_{i+\frac{1}{2}}$;
  - 否:执行后续判定.
- 是否满足:$f(x_i)·f(x_{i+1})<0$
  - 是:在区间$[x_i,x_{i+1}]$上通过二分法得到近似根$x_{i+\frac{1}{2}}$;
  - 否:继续向后判定是否满足:$f(x_i)·f(x_{i+2})<0$,直到完成对整个区间$[a,b]$的判定,退出循环.
Step3: 选择近似根$x_{i+\frac{1}{2}}$的邻近点$x_{i+\frac{1}{2}}^+$或者$x_{i+\frac{1}{2}}^-$与$x_{i+2}$配对执行二分法.
Step4: 继续执行 Step2-Step3 ,判断是否能够找到$m$个满足条件的根.
- 是:输出结果;
- 否:加密网格($h=\frac{h}{2}$).
Step5: 继续执行 Step2-Step3 ,直到找到$m$个满足条件的根.

利用二分法(Bisection Method)求解在区间$[a,b]$上存在$m$个实根的方程$f(x)=0$的

```Python
# 开发者:    Leo 刘
# 开发环境: macOs Big Sur
# 开发时间: 2022/1/4 4:55 下午
# 邮箱  : 517093978@qq.com
# @Software: PyCharm
# ----------------------------------------------------------------------------------------------------------
"""
    主函数功能：
    寻找f(x)在指定区间[a,b]上的所有根
    输出区间端点函数值
    绘制函数图像
"""
import numpy as np
import matplotlib.pyplot as plt


def fun(x):
    # 方程等号左边函数f(x)
    f = 54 * x ** 6 + 45 * x ** 5 - 102 * x ** 4 - 69 * x ** 3 + 35 * x ** 2 + 16 * x - 4
    return f


def sign(val):
    # 符号函数

    if val < 0:
        s = "-"

    elif val > 0:
        s = "+"

    else:
        s = "0"

    return s


def main(a, b, step=0.0001):
    i = 0
    roots = []
    roots_interval = []
    root_counter = 0
    signs = ""
    # 打印f(x)的符号
    print("-" * 38)
    # print("近似解x\t\t\t函数值\t\t函数值符号")
    for x in np.arange(a, b, step):
        # print("-" * 38)
        val = fun(x)
        signs = signs + sign(val)
        # print("%.6f \t\t%.6f\t\t %s" % (x, val, sign(val)))
        if i > 0 and (signs[i - 1] == 0 or signs[i - 1] != signs[i]):
            root_counter += 1
            if signs[i - 1] == '0':
                roots = np.append(roots, x - step)
            if signs[i - 1] != signs[i] and signs[i - 1] != '0':
                roots_interval = np.append(roots_interval, x)
        i += 1

    # print("-" * 38)
    print("方程在区间[%.4f,%.4f]上根的个数为：%d" % (a, b, root_counter))
    print("准确解%d个，分别为:" % len(roots), roots)
    print("近似解%d个，所在区间分别为:" % len(roots_interval))
    for k in range(len(roots_interval)):
        print("[%.6f,%.6f]  " % (roots_interval[k] - step, roots_interval[k]), end='')

    #  绘图
    plt.figure(figsize=(8, 4))
    plt.plot(np.arange(a, b, step), np.zeros_like(np.arange(a, b, step)), "k")
    plt.plot(np.arange(a, b, step), fun(np.arange(a, b, step)), "b", label="$f(x)$")

    plt.xlabel("$x$")
    plt.ylabel("$f(x)$")
    plt.title("Example")

    plt.ylim(-2, 2)
    plt.legend()  # 显示左下角的图例

    plt.show()
    return root_counter


if __name__ == '__main__':
    main(-2, 2)

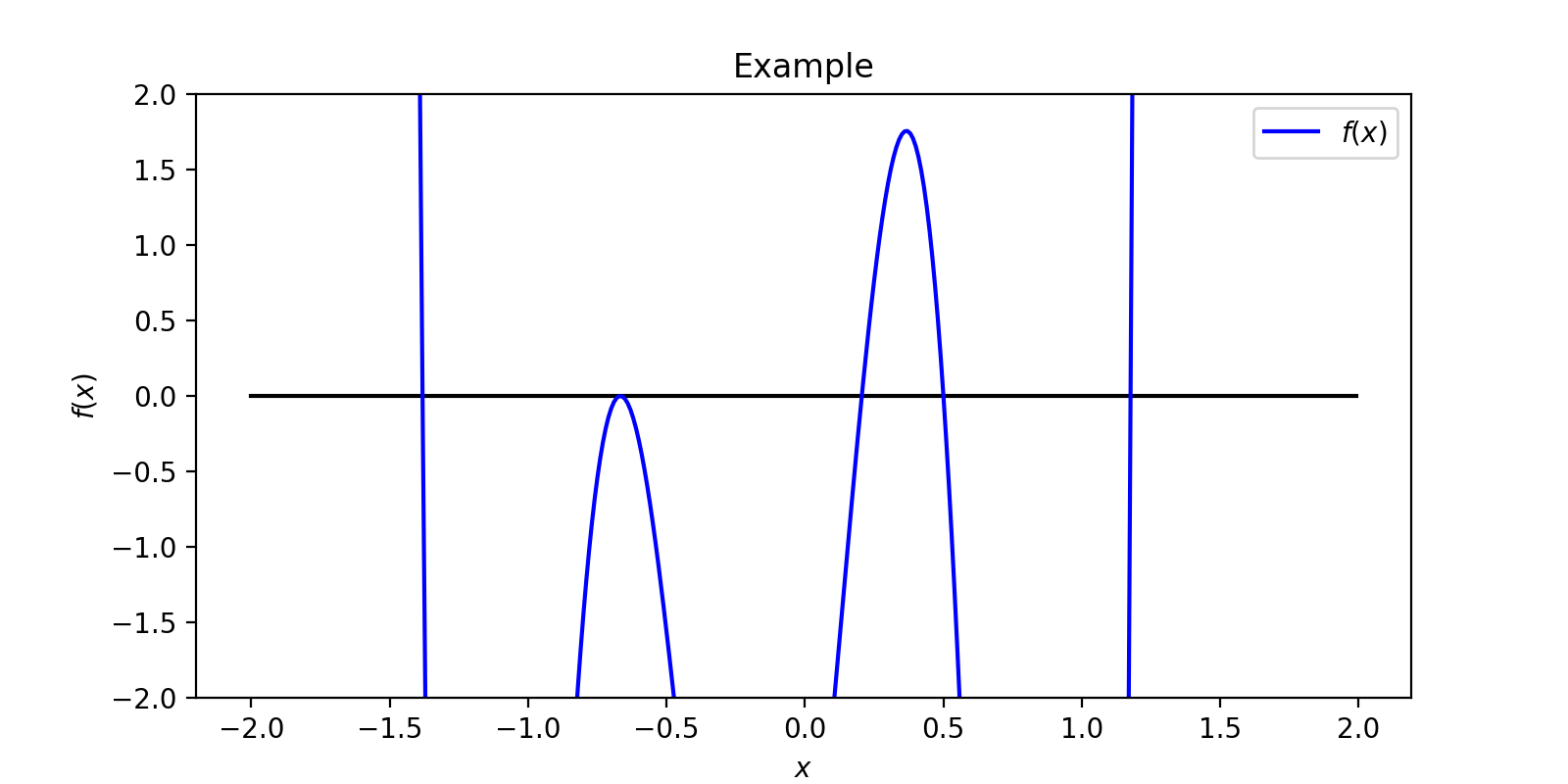
程序运行结果: Figure_1

方程在区间[-2.0000,2.0000]上根的个数为：5
准确解0个，分别为: []
近似解5个，所在区间分别为:
[-1.381300,-1.381200]  [-0.666900,-0.666400]  [0.205100,0.205200]  [0.500000,0.500100]  [1.176100,1.176200]

从程序运行结果可以看到,该方程在 $[-2,2]$ 有5个根,根所在区间分别为[-1.381300,-1.381200]、[-0.666900,-0.666400]、[0.205100,0.205200]、[0.500000,0.500100]、[1.176100,1.176200]

下面使用经典Newton迭代法分别选取不同初值(-1.3813、-0.6669、0.2051、0.5000、1.1761)计算结果

Python程序源代码

# 开发者:    Leo 刘
# 开发环境: macOs Big Sur
# 开发时间: 2022/1/4 5:12 下午
# 邮箱  : 517093978@qq.com
# @Software: PyCharm
# ----------------------------------------------------------------------------------------------------------
from sympy import *
import matplotlib.pyplot as plt

x = symbols('x')
x0 = -1.3813
x_list = [x0]
x_values = []
y_values = []
i = 0


def f(x):
    # f = x * exp(x) - 1
    f = 54 * x ** 6 + 45 * x ** 5 - 102 * x ** 4 - 69 * x ** 3 + 35 * x ** 2 + 16 * x - 4
    return f


while True:
    if diff(f(x), x).subs(x, x0) == 0:
        print('极值点：', x0)
        break
    else:
        x0 = x0 - f(x0) / diff(f(x), x).subs(x, x0)
        x_list.append(x0)
    if len(x_list) > 1:
        i += 1
        error = abs((x_list[-1] - x_list[-2]) / x_list[-1])
        x_values.append(i)
        y_values.append(error)
        if error == 0:
            print(f'迭代第{i}次后，误差为0')
            break
    else:
        pass

print(f'所求方程式的根为{x_list[-1]}')

# 设置绘图风格
plt.style.use('ggplot')
# 处理中文乱码
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
# 坐标轴负号的处理
plt.rcParams['axes.unicode_minus'] = False
# 横坐标是迭代次数
# 纵坐标是误差值
plt.plot(x_values,
         y_values,
         color='steelblue',  # 折线颜色
         marker='o',  # 折线图中添加圆点
         markersize=3,  # 点的大小
         )
# 修改x轴和y轴标签
plt.xlabel('Number of iterations')
plt.ylabel('Difference')
# 显示图形
plt.show()

程序运行结果:

初值:-1.3813

迭代至电脑默认为误差为0为止结果:

1 2	`迭代第3次后，误差为0 所求方程式的根为-1.38129848204399`

迭代图

Figure_1 初值:-0.6669

迭代至电脑默认为误差为0为止结果:

1 2	`迭代第18次后，误差为0 所求方程式的根为-0.666666669320183`

迭代图

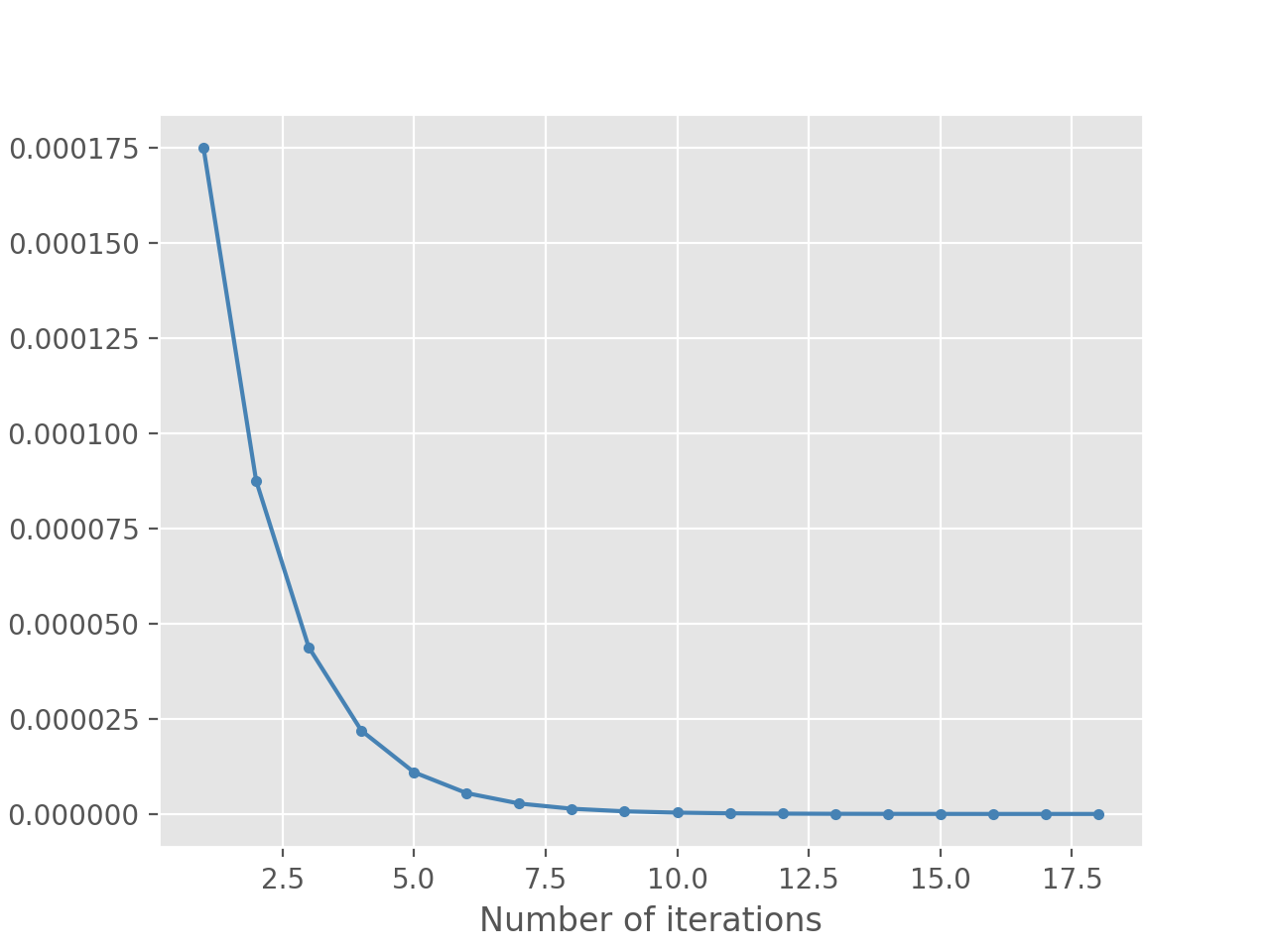
初值:0.2051

迭代至电脑默认为误差为0为止结果:

1 2	`迭代第4次后，误差为0 所求方程式的根为0.205182924689048`

迭代图

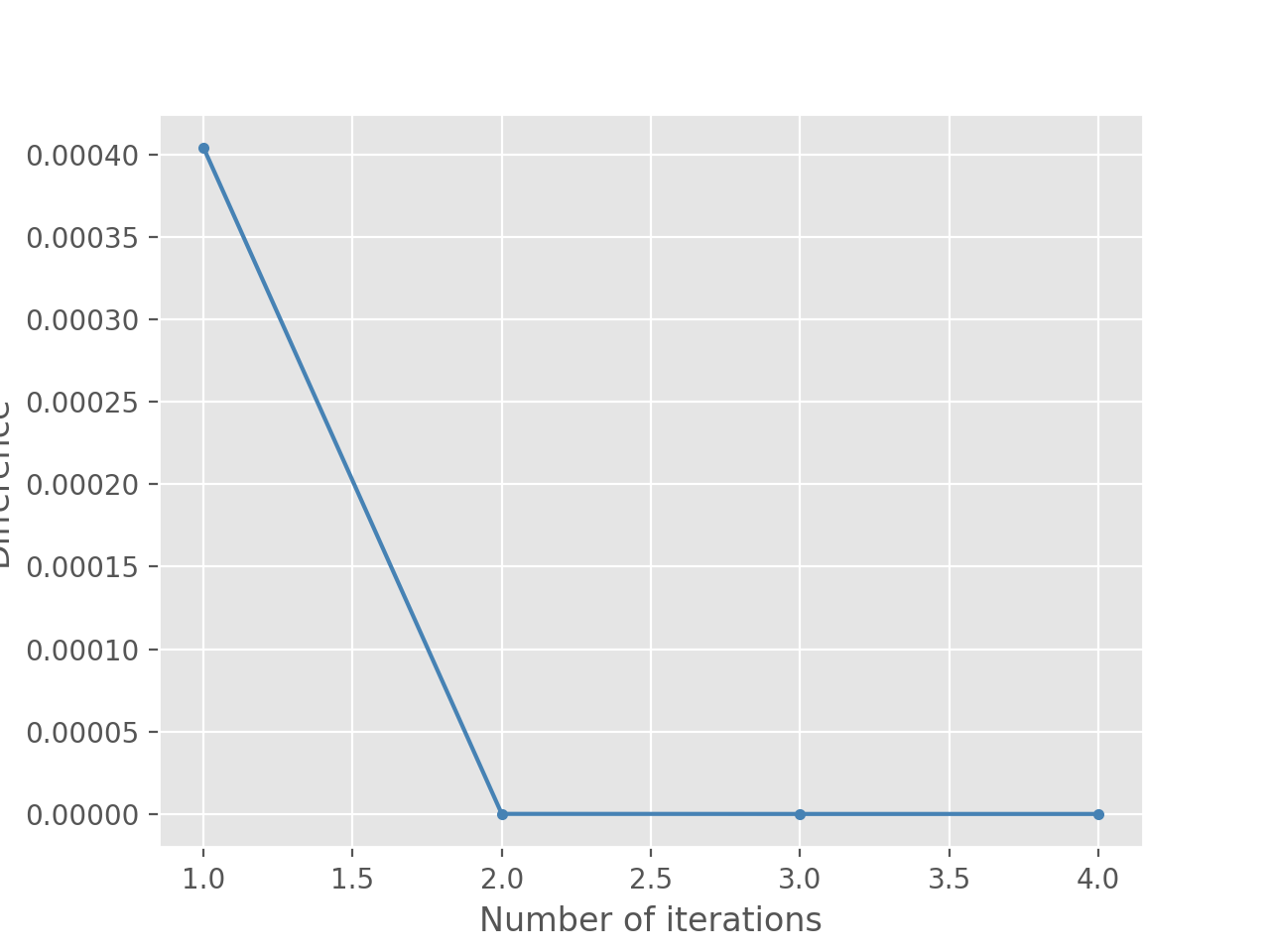Figure_1 初值:0.5000

迭代至电脑默认为误差为0为止结果:

1 2	`迭代第1次后，误差为0 所求方程式的根为0.500000000000000`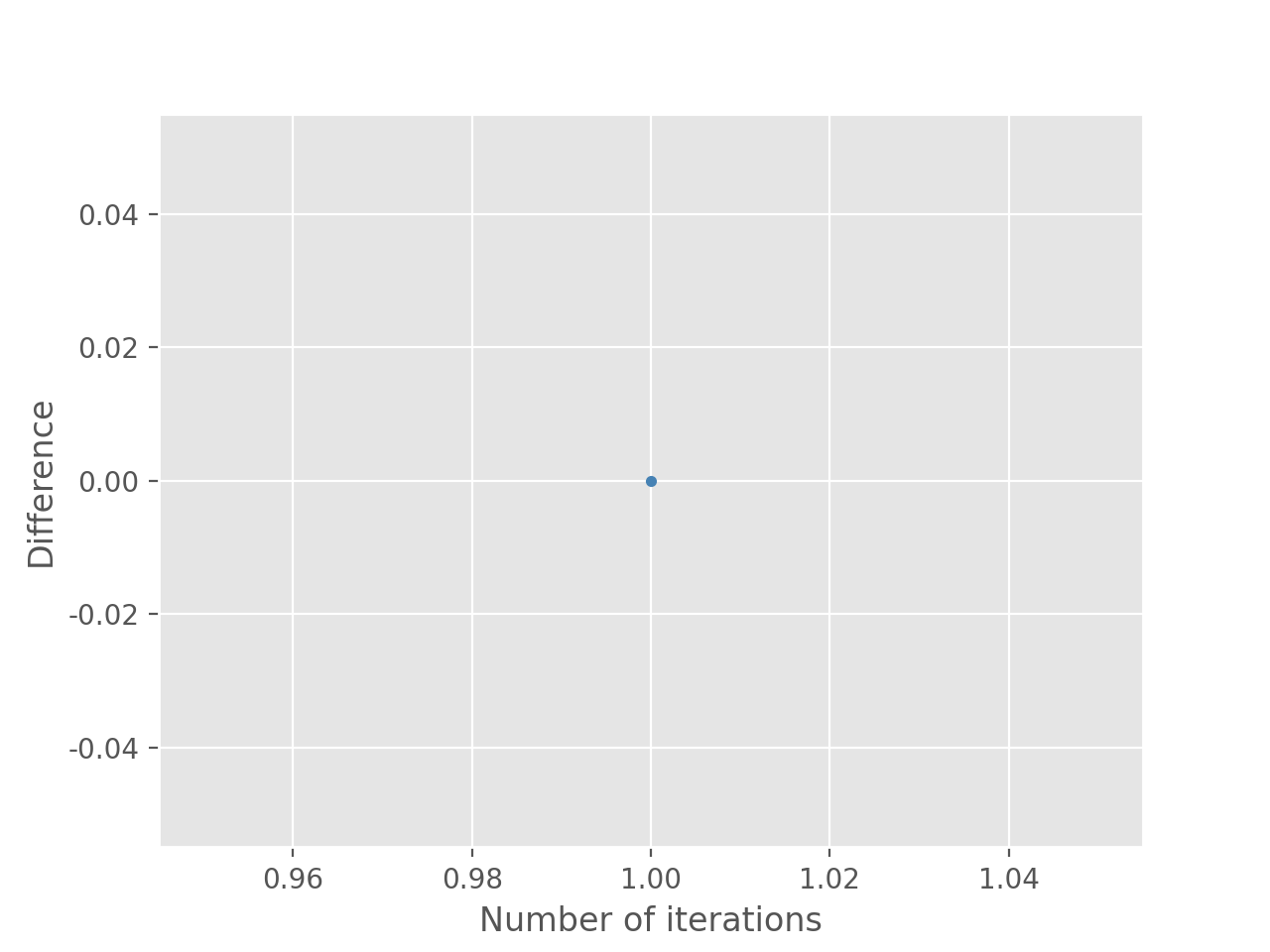

迭代图

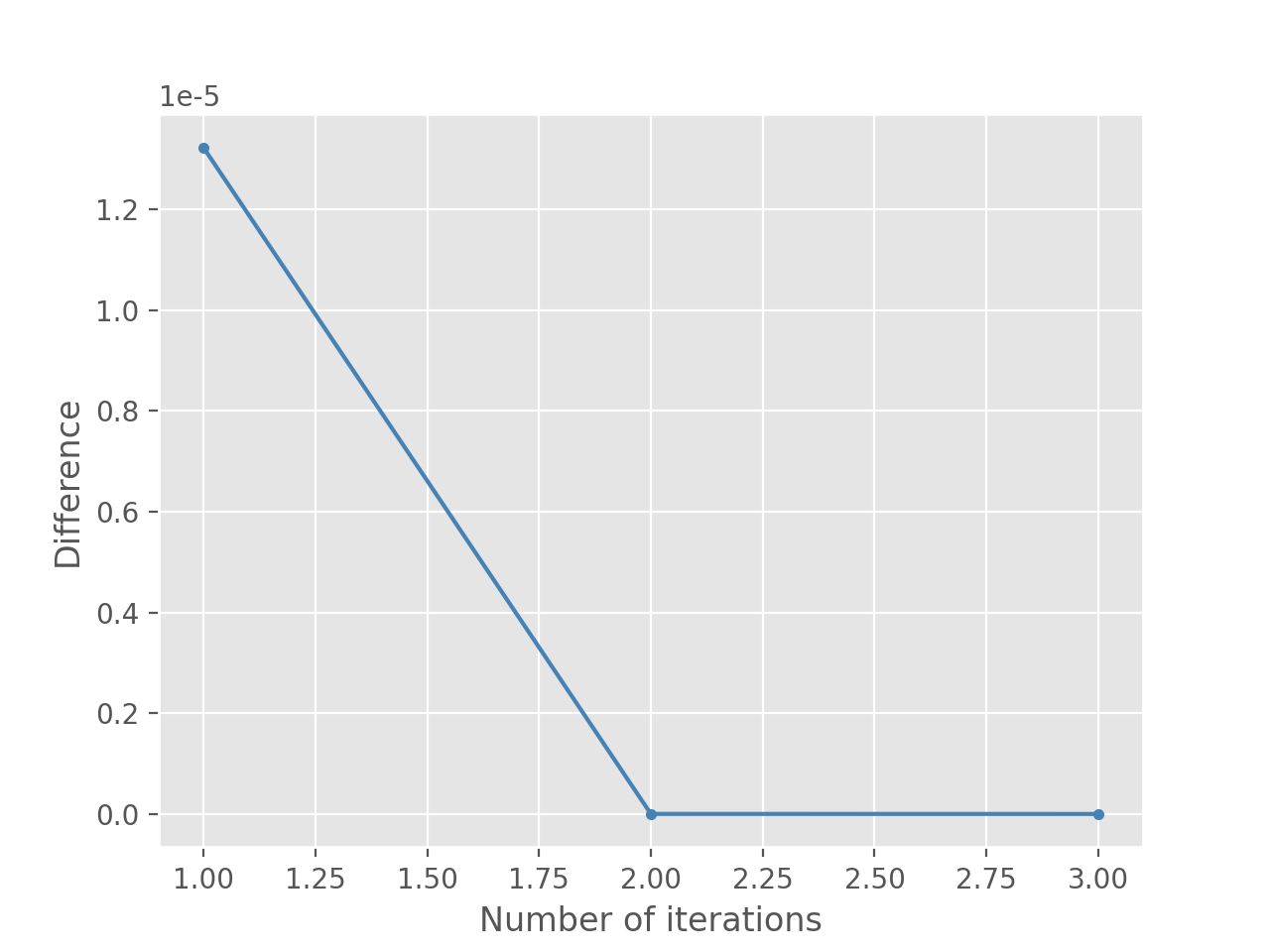
初值:1.1761

迭代至电脑默认为误差为0为止结果:

1 2	`迭代第3次后，误差为0 所求方程式的根为1.17611555735495`

迭代图

结果分析:

至此,已完成对方程的求根,从程序运行结果可以看出,在真实解的附近给定初值,Newton法可以很快的收敛到给定初值附近的根,效果较好.

设 $p$ 是函数 $f(x)=0$ 的根, $p$ 的阶 $M=2(p$ 是二重根 $)$ .证明加速牛顿-拉夫森迭代 \[ p_{k}=p_{k-1}-2 \frac{f\left(p_{k-1}\right)}{f^{\prime}\left(p_{k-1}\right)} \] 的收敛阶是二阶的.(10 分)

解答

定义 $3.1$ 若存在 $M>0$, \[ \lim _{k \rightarrow \infty} \frac{\left|e_{k+1}\right|}{\left|e_{k}\right|^{n}}=\lim _{k \rightarrow \infty} \frac{\left|x_{k+1}-\alpha\right|}{\left|x_{k}-\alpha\right|^{n}}=M \] 称迭代格式收敛的阶为 $n$. 分析 Newton 迭代法收敛的阶: \[ \begin{aligned} x_{k+1}-\alpha &=\varphi\left(x_{k}\right)-\varphi(\alpha)=\varphi(\alpha)+\left(x_{k}-\alpha\right) \varphi^{\prime}(\alpha)+\frac{\left(x_{k}-\alpha\right)^{2}}{2 !} \varphi^{\prime \prime}(\xi)-\varphi(\alpha) \\ &=\frac{\left(x_{k}-\alpha\right)^{2}}{2 !} \varphi^{\prime \prime}(\xi) \end{aligned} \] \[\lim _{k \rightarrow \infty} \frac{\left|x_{k+1}-\alpha\right|}{\left|x_{k}-\alpha\right|^{2}} =\lim _{k \rightarrow \infty} \frac{\left|e_{k+1}\right|}{\left|e_{k}\right|^{2}}=\varphi^{\prime \prime}(\alpha)\] 因此求单根 Newton 迭代是二阶迭代方法.

设 $\alpha$ 为 $f(x)$ 的 $p$ 重根时, 记 \[ \begin{gathered} f(x)=(x-\alpha)^{p} h(x) \\ \varphi(x)=x-\frac{(x-\alpha)^{p} h(x)}{p(x-\alpha)^{p-1} h(x)+(x-\alpha)^{p} h^{\prime}(x)} \\ \varphi(x)=x-\frac{(x-\alpha)h(x)}{p h(x)+(x-\alpha) h^{\prime}(x)} \\ \varphi^{\prime}(x)=\frac{\left(1-\frac{1}{p}\right)+(x-\alpha) \frac{2 h^{\prime}(x)}{p h(x)}+(x-\alpha)^{2} \frac{h^{\prime \prime}(x)}{p^{2} h(x)}}{\left[1+(x-\alpha) \frac{h^{\prime}(x)}{p h(x)}\right]^{2}} \\ \varphi^{\prime}(\alpha)=1-\frac{1}{p} \end{gathered} \] 仍然有 \[\left|\varphi^{\prime}(\alpha)\right|<1\] 当初始值在根 $\alpha$ 附近, 迭代也收敛, 这是一阶迭代方法, 收敛因子为 $1-\frac{1}{p}$.

若 $\alpha$ 为 $f(x)$ 的 $p$ 重根时, 这时取下面迭代格式 \[ x_{k+1}=x_{k}-p \frac{f\left(x_{k}\right)}{f^{\prime}\left(x_{k}\right)}, \quad k=1,2, \cdots \]

此时 \[ \begin{gathered} \varphi(x)=x-\frac{p(x-\alpha)^{p} h(x)}{p(x-\alpha)^{p-1} h(x)+(x-\alpha)^{p} h^{\prime}(x)} \\ \varphi(x)=x-\frac{p(x-\alpha)h(x)}{p h(x)+(x-\alpha) h^{\prime}(x)} \\ \varphi^{\prime}(x)=\frac{\left(1-\frac{1}{1}\right)+(x-\alpha) \frac{2 h^{\prime}(x)}{h(x)}+(x-\alpha)^{2} \frac{h^{\prime \prime}(x)}{p h(x)}}{\left[1+(x-\alpha) \frac{h^{\prime}(x)}{p h(x)}\right]^{2}} \\ \varphi^{\prime}(\alpha)=1-\frac{1}{1}=0 \end{gathered} \]

可以发现修正之后迭代函数一阶导数等于 0，也就是算法至少是2阶收敛.

分析加速牛顿-拉夫森迭代法收敛的阶:

此时$p=2$, $\alpha$为$f(x)$的二重根. \[ \begin{aligned} x_{k+1}-\alpha &=\varphi\left(x_{k}\right)-\varphi(\alpha)=\varphi(\alpha)+\left(x_{k}-\alpha\right) \varphi^{\prime}(\alpha)+\frac{\left(x_{k}-\alpha\right)^{2}}{2 !} \varphi^{\prime \prime}(\xi)-\varphi(\alpha) \\ &=\frac{\left(x_{k}-\alpha\right)^{2}}{2 !} \varphi^{\prime \prime}(\xi) \end{aligned} \] \[\lim _{k \rightarrow \infty} \frac{\left|x_{k+1}-\alpha\right|}{\left|x_{k}-\alpha\right|^{2}} =\lim _{k \rightarrow \infty} \frac{\left|e_{k+1}\right|}{\left|e_{k}\right|^{2}}=\varphi^{\prime \prime}(\alpha)\] 因此该加速 Newton 迭代是二阶迭代方法.

参考资料: 张韵华.《数值计算方法与算法》第三版.科学出版社

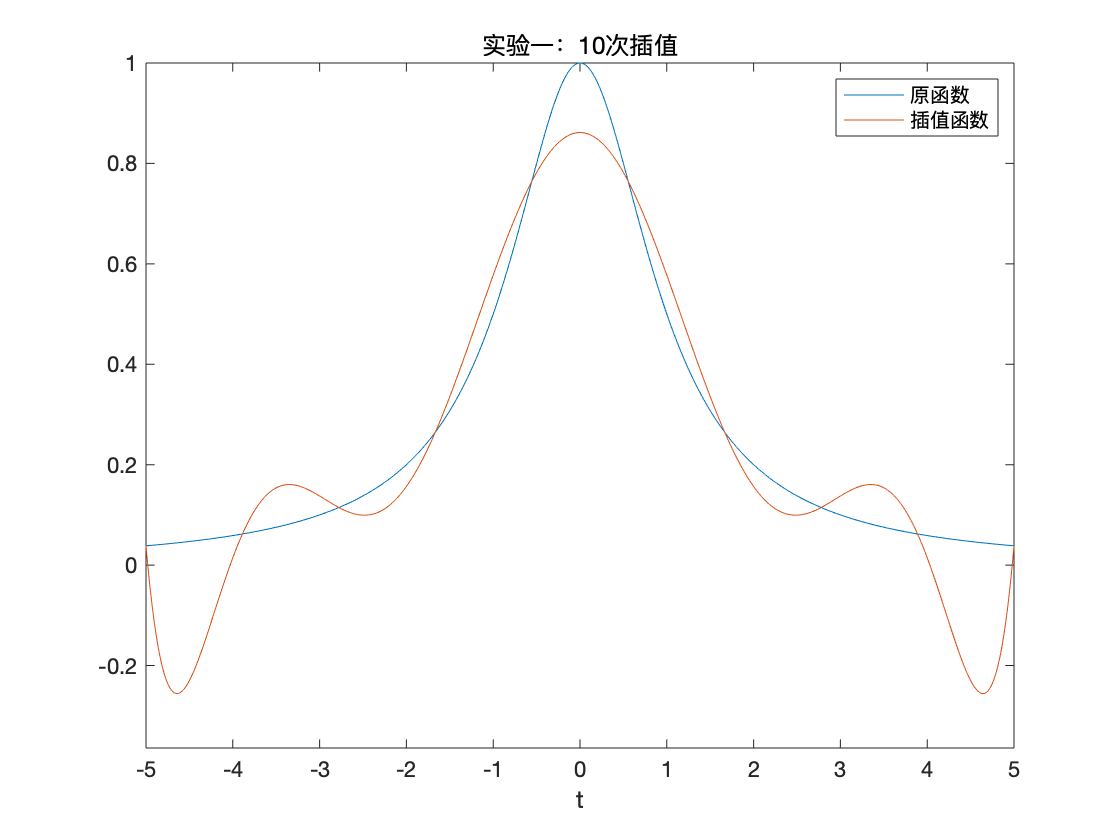
五、（10 分）对 $[-5,5]$ 做等距划分, $x_{i}=-5+i h, h=\frac{10}{n}(i=0,1, \ldots, n)$, 并对 $Runge$ 给出的函数 $y=\frac{1}{1+x^{2}}$ 做 $Lagrange$ 插值和三次样条插值, 观察 $Runge$ 现象的发生与防止.（通过计算机编程完成下列问题, 请画出函数的曲线和插值函数的曲线图, 并将数值计算结果用列表的形式展示.)

取 $\mathrm{n}=10,20$ 做 $Lagrange$ 插值 $L_{10}(x), L_{20}(x)$ .

解答

MATLAB程序代码

clear
n=10;  %10,15插值点数
syms t;

x = linspace(-5,5,n);
y=f(x);
for i=1:n
L(i)=Lagrange(x,n,i,t);
end
LN=sum(y.*L);
t=-5:0.01:5;
y0=1./(1+t.^2);
 plot(t,y0);
 hold on;
 ezplot(LN,t);
 a=strcat('实验一：',num2str(n),'次插值');
 title(a);
 legend('原函数','插值函数');

function fi=Lagrange(x,n,i,t)

fu=1;
fd=1;

for  j=1:n                      %循环计算 
         if i~=j
             fu=fu.*(t-x(j));
             fd=fd.*(x(i)-x(j));
         end
end
fi=fu/fd;
end
  
function y=f(x)
y=1./(1+x.^2);
end

数值算例

$S_{10}(x)$

函数的曲线和插值函数的曲线图

untitled 插值多项式:

(2783138807808*(t - 5)*(t + 5)*(t - 5/3)*(t + 5/3)*(t - 5/9)*(t + 5/9)*(t - 25/9)*(t + 25/9)*(t - 35/9))/4670151439004235371 - (347892350976*(t - 5)*(t + 5)*(t - 5/3)*(t + 5/3)*(t - 5/9)*(t + 5/9)*(t - 25/9)*(t + 25/9)*(t + 35/9))/583768929875529503 - (1391569403904*(t - 5)*(t + 5)*(t - 5/3)*(t + 5/3)*(t - 5/9)*(t + 5/9)*(t - 25/9)*(t - 35/9)*(t + 35/9))/315574934526894203 + (11132555231232*(t - 5)*(t + 5)*(t - 5/3)*(t + 5/3)*(t - 5/9)*(t + 5/9)*(t + 25/9)*(t - 35/9)*(t + 35/9))/2524599476215153271 - (14843406974976*(t - 5)*(t + 5)*(t - 5/3)*(t + 5/3)*(t - 5/9)*(t - 25/9)*(t + 25/9)*(t - 35/9)*(t + 35/9))/144399052733741401 + (44530220924928*(t - 5)*(t + 5)*(t - 5/3)*(t + 5/3)*(t + 5/9)*(t - 25/9)*(t + 25/9)*(t - 35/9)*(t + 35/9))/433197158201224097 + (51539607552*(t - 5)*(t + 5)*(t - 5/3)*(t - 5/9)*(t + 5/9)*(t - 25/9)*(t + 25/9)*(t - 35/9)*(t + 35/9))/2171094248060381 - (2473901162496*(t - 5)*(t + 5)*(t + 5/3)*(t - 5/9)*(t + 5/9)*(t - 25/9)*(t + 25/9)*(t - 35/9)*(t + 35/9))/104212523906898271 - (1073741824*(t - 5)*(t - 5/3)*(t + 5/3)*(t - 5/9)*(t + 5/9)*(t - 25/9)*(t + 25/9)*(t - 35/9)*(t + 35/9))/26148914546491945 + (4294967296*(t + 5)*(t - 5/3)*(t + 5/3)*(t - 5/9)*(t + 5/9)*(t - 25/9)*(t + 25/9)*(t - 35/9)*(t + 35/9))/104595658185967767

数值算例

$S_{20}(x)$

函数的曲线和插值函数的曲线图

untitled 插值多项式:

23658496*(t - 5)*(t + 5)*(t - 5/19)*(t + 5/19)*(t - 15/19)*(t + 15/19)*(t - 25/19)*(t + 25/19)*(t - 35/19)*(t + 35/19)*(t - 45/19)*(t + 45/19)*(t - 55/19)*(t + 55/19)*(t - 65/19)*(t + 65/19)*(t - 75/19)*(t + 75/19)*(t - 85/19)

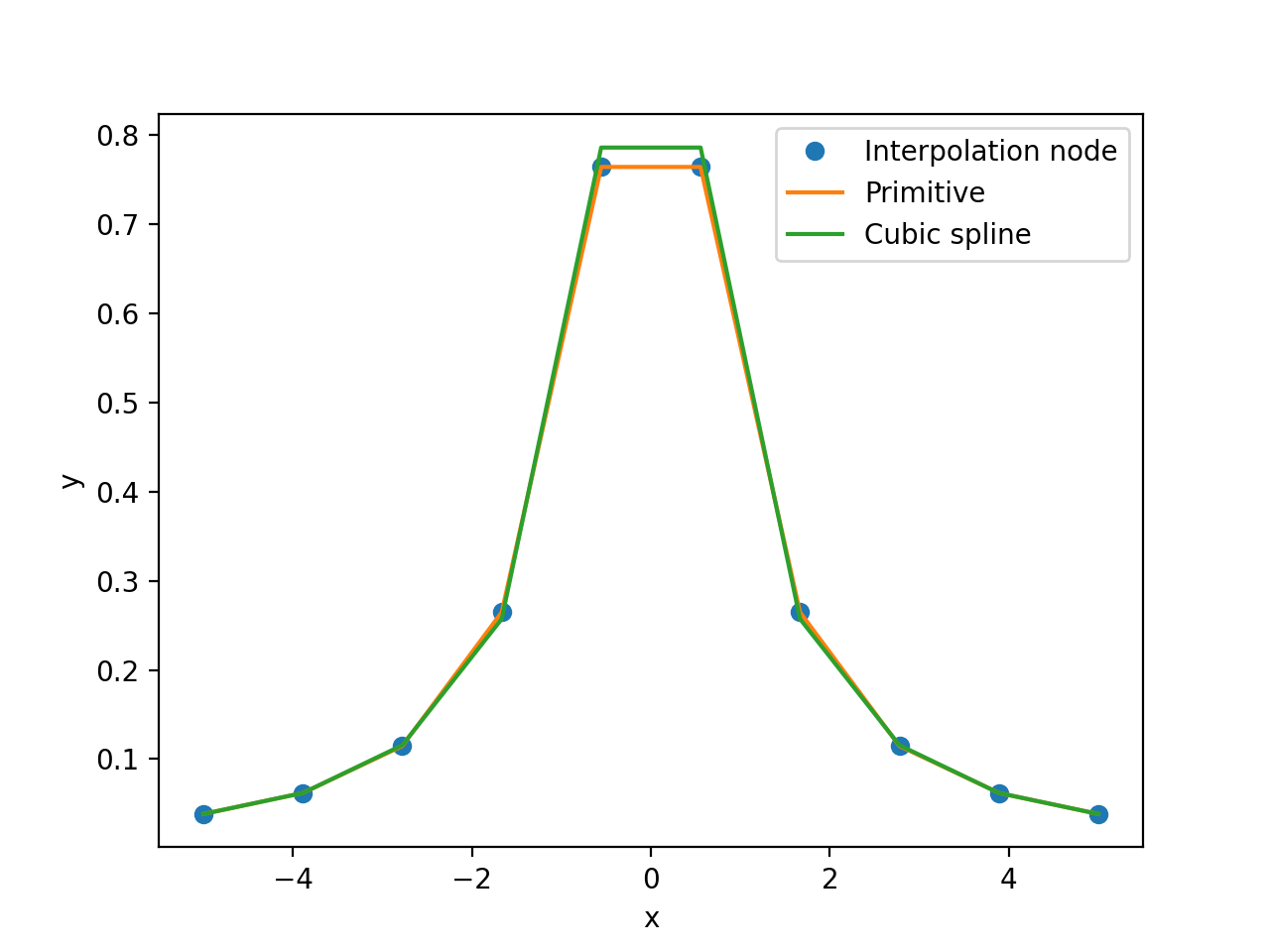
取 $n=10,20$ 做第一种边界条件的三次样条插值 $S_{10}(x), S_{20}(x)$ .

解答

这里假设第一种边界条件的数值均为自由边界.即 $f'(x_0) = \frac{5}{338}$ $ f'(x_n) =-$ 的情况.

Python程序代码

# 开发者:    Leo 刘
# 开发环境: macOs Big Sur
# 开发时间: 2022/1/4 6:15 下午
# 邮箱  : 517093978@qq.com
# @Software: PyCharm
# ----------------------------------------------------------------------------------------------------------
import numpy as np
from sympy import *
import matplotlib.pyplot as plt

# 这里假设数值均为1.即 f'(x_0) = f'(x_n) = 1 的情况

N = 20
a_0 = 0.0149929
a_n = -0.0149929


def f(x):
    return 1 / (1 + x ** 2)


def cal(begin, end, i):
    by = f(begin)
    ey = f(end)
    I = Ms[i] * ((end - n) ** 3) / 6 + Ms[i + 1] * ((n - begin) ** 3) / 6 + (by - Ms[i] / 6) * (end - n) + (
            ey - Ms[i + 1] / 6) * (n - begin)
    return I


def ff(x):  # f[x0, x1, ..., xk]
    ans = 0
    for i in range(len(x)):
        temp = 1
        for j in range(len(x)):
            if i != j:
                temp *= (x[i] - x[j])
        ans += f(x[i]) / temp
    return ans


def calM():
    lam = [1] + [1 / 2] * 9
    miu = [1 / 2] * 9 + [1]
    # Y = 1 / (1 + n ** 2)
    # df = diff(Y, n)
    x = np.array(range(11)) - 5
    # ds = [6 * (ff(x[0:2]) - df.subs(n, x[0]))]
    ds = [6 * (ff(x[0:2]) - a_0)]
    for i in range(9):
        ds.append(6 * ff(x[i: i + 3]))
    # ds.append(6 * (df.subs(n, x[10]) - ff(x[-2:])))
    ds.append(6 * (a_n - ff(x[-2:])))
    Mat = np.eye(11, 11) * 2
    for i in range(11):
        if i == 0:
            Mat[i][1] = lam[i]
        elif i == 10:
            Mat[i][9] = miu[i - 1]
        else:
            Mat[i][i - 1] = miu[i - 1]
            Mat[i][i + 1] = lam[i]
    ds = np.mat(ds)
    Mat = np.mat(Mat)
    Ms = ds * Mat.I
    return Ms.tolist()[0]


def calnf(x):
    nf = []
    for i in range(len(x) - 1):
        nf.append(cal(x[i], x[i + 1], i))
    return nf


def calf(f, x):
    y = []
    for i in x:
        y.append(f.subs(n, i))
    return y


def nfSub(x, nf):
    tempx = np.array(range(11)) - 5
    dx = []
    for i in range(10):
        labelx = []
        for j in range(len(x)):
            if tempx[i] <= x[j] < tempx[i + 1]:
                labelx.append(x[j])
            elif i == 9 and tempx[i] <= x[j] <= tempx[i + 1]:
                labelx.append(x[j])
        dx = dx + calf(nf[i], labelx)
    return np.array(dx)


def draw(nf):
    # plt.rcParams['font.sans-serif'] = ['SimHei']
    # plt.rcParams['axes.unicode_minus'] = False
    x = np.linspace(-5, 5, N)
    y = f(x)
    Ly = nfSub(x, nf)
    print("真实值和三次样条插值数值结果对比".center(50))
    print('-' * 60)
    print("xi\t\t", "   True_solution\t", " Cubic spline\t\t", "error")
    for i in range(len(x)):
        print('-' * 60)
        print("%.2f\t\t" % x[i],
              "%.7f\t\t" % f(x[i]),
              "%.7f\t\t" % Ly[i],
              "%.7f\t\t" % abs(f(x[i]) - Ly[i]),
              )
    print('-' * 60)
    plt.plot(x, y, 'o', label='Interpolation node')
    plt.plot(x, y, label='Primitive')
    plt.plot(x, Ly, label='Cubic spline')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.legend()

    plt.savefig('1.png')
    plt.show()


#
def lossCal(nf):
    x = np.linspace(-5, 5, N)
    y = f(x)
    Ly = nfSub(x, nf)
    Ly = np.array(Ly)
    temp = Ly - y
    temp = abs(temp)
    print('均方误差：', temp.mean())


def loss_x0(nf):
    x = np.array([4.8])
    y = f(x)
    Ly = nfSub(x, nf)
    Ly = np.array(Ly)
    temp = Ly - y
    temp = abs(temp)
    print("xi\t\t", "   True_solution\t", " Cubic spline\t\t", "error")
    for i in range(len(x)):
        print('-' * 60)
        print("%.2f\t\t" % x[i],
              "%.7f\t\t" % f(x[i]),
              "%.7f\t\t" % Ly[i],
              "%.7f\t\t" % abs(f(x[i]) - Ly[i]),
              )
    print('-' * 60)


if __name__ == '__main__':
    x = np.array(range(11)) - 5
    y = f(x)

    n, m = symbols('n m')
    init_printing(use_unicode=True)
    Ms = calM()
    nf = calnf(x)
    draw(nf)
    lossCal(nf)
    loss_x0(nf)

数值算例

$S_{10}(x)$

函数的曲线和插值函数的曲线图

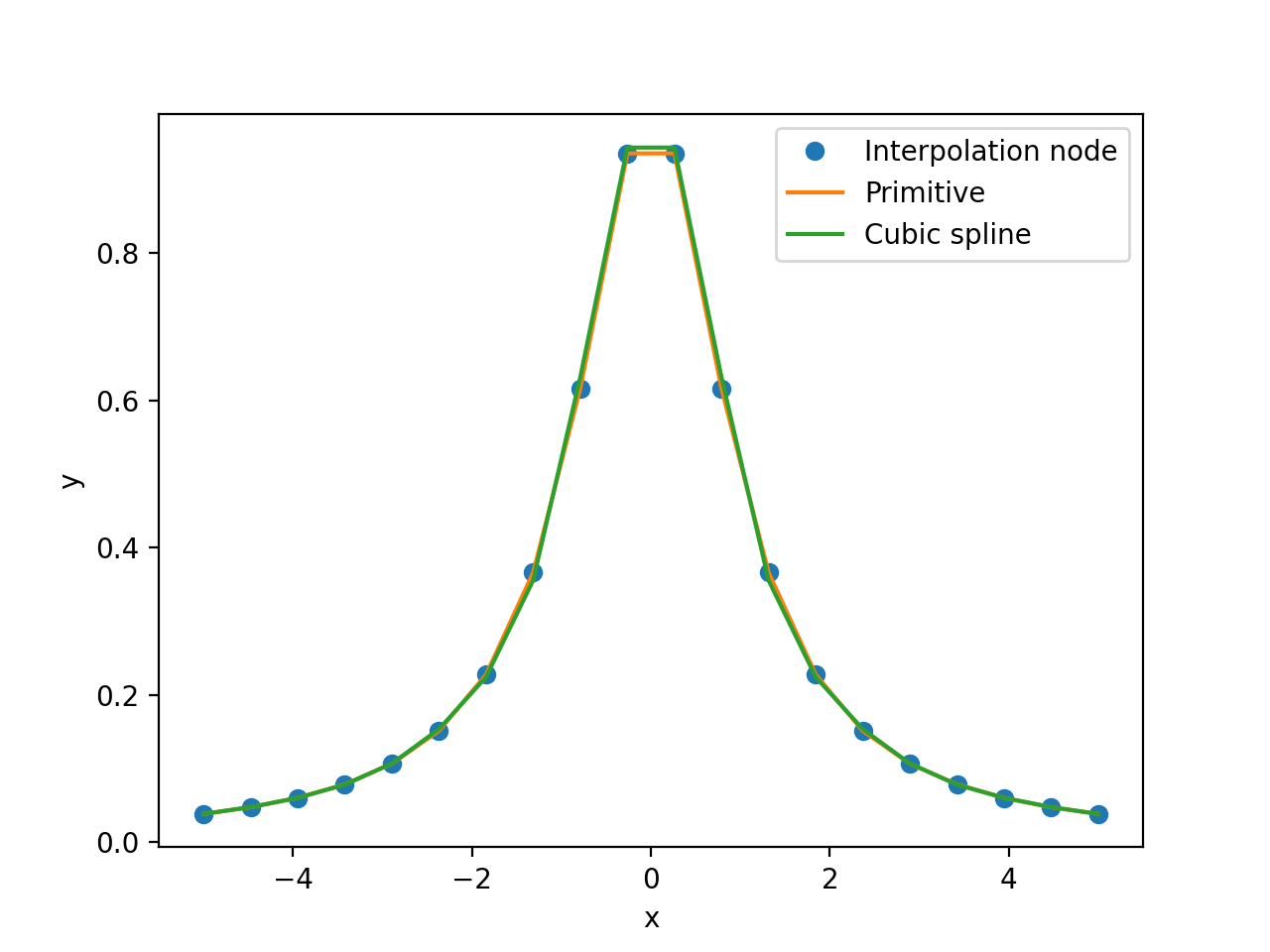
Figure_1 数值计算结果

                 真实值和三次样条插值数值结果对比                 
------------------------------------------------------------
xi		    True_solution	  Cubic spline		 error
------------------------------------------------------------
-5.00		 0.0384615		 0.0384615		 0.0000000		
------------------------------------------------------------
-3.89		 0.0620214		 0.0619991		 0.0000223		
------------------------------------------------------------
-2.78		 0.1147309		 0.1156028		 0.0008719		
------------------------------------------------------------
-1.67		 0.2647059		 0.2571958		 0.0075101		
------------------------------------------------------------
-0.56		 0.7641509		 0.7858994		 0.0217484		
------------------------------------------------------------
0.56		 0.7641509		 0.7858994		 0.0217484		
------------------------------------------------------------
1.67		 0.2647059		 0.2571958		 0.0075101		
------------------------------------------------------------
2.78		 0.1147309		 0.1156028		 0.0008719		
------------------------------------------------------------
3.89		 0.0620214		 0.0619991		 0.0000223		
------------------------------------------------------------
5.00		 0.0384615		 0.0384615		 0.0000000		
------------------------------------------------------------
均方误差： 0.00603055680210736
xi		    True_solution	  Cubic spline		 error
------------------------------------------------------------
4.80		 0.0415973		 0.0415813		 0.0000160		
------------------------------------------------------------

$S_{20}(x)$

函数的曲线和插值函数的曲线图

数值计算结果

                 真实值和三次样条插值数值结果对比                 
------------------------------------------------------------
xi		    True_solution	  Cubic spline		 error
------------------------------------------------------------
-5.00		 0.0384615		 0.0384615		 0.0000000		
------------------------------------------------------------
-4.47		 0.0475877		 0.0477604		 0.0001727		
------------------------------------------------------------
-3.95		 0.0603074		 0.0603095		 0.0000022		
------------------------------------------------------------
-3.42		 0.0787178		 0.0782141		 0.0005037		
------------------------------------------------------------
-2.89		 0.1066155		 0.1069884		 0.0003729		
------------------------------------------------------------
-2.37		 0.1512992		 0.1536492		 0.0023500		
------------------------------------------------------------
-1.84		 0.2276166		 0.2242619		 0.0033547		
------------------------------------------------------------
-1.32		 0.3661258		 0.3555038		 0.0106220		
------------------------------------------------------------
-0.79		 0.6160410		 0.6311832		 0.0151423		
------------------------------------------------------------
-0.26		 0.9352332		 0.9431363		 0.0079032		
------------------------------------------------------------
0.26		 0.9352332		 0.9431363		 0.0079032		
------------------------------------------------------------
0.79		 0.6160410		 0.6311832		 0.0151423		
------------------------------------------------------------
1.32		 0.3661258		 0.3555038		 0.0106220		
------------------------------------------------------------
1.84		 0.2276166		 0.2242619		 0.0033547		
------------------------------------------------------------
2.37		 0.1512992		 0.1536492		 0.0023500		
------------------------------------------------------------
2.89		 0.1066155		 0.1069884		 0.0003729		
------------------------------------------------------------
3.42		 0.0787178		 0.0782141		 0.0005037		
------------------------------------------------------------
3.95		 0.0603074		 0.0603095		 0.0000022		
------------------------------------------------------------
4.47		 0.0475877		 0.0477604		 0.0001727		
------------------------------------------------------------
5.00		 0.0384615		 0.0384615		 0.0000000		
------------------------------------------------------------
均方误差： 0.00404236524270380
xi		    True_solution	  Cubic spline		 error
------------------------------------------------------------
4.80		 0.0415973		 0.0415813		 0.0000160		
------------------------------------------------------------

考察上述两种插值在 $x=4.8$ 处的误差, 并分析.

在 $x=4.8$ 处,真实值和 Lagrange 插值数值结果对比

在 $x=4.8$ 处,真实值和三次样条插值数值结果对比

xi		    True_solution	  Cubic spline		 error
------------------------------------------------------------
4.80		 0.0415973		 0.0415813		 0.0000160		
------------------------------------------------------------
xi		    True_solution	  Cubic spline		 error
------------------------------------------------------------
4.80		 0.0415973		 0.0415813		 0.0000160		
------------------------------------------------------------

从输出图像及误差看容易出，

Lagrange 插值在插值区间中部 Lagrange 插值多项式与原 Runge 函数符合得较好；但在插值区间的两端两者的差别很大（Lagrange 在区间$[-5,-4.9]$的最小值为-59.7819），此时的插值余项不满足要求，因此用等距 20 次 Lagrange 插值多项式来对 Runge 函数在区间$[-5,5]$做插值逼近并不合适，会出现明显的 Runge 现象.
三次样条插值的结果比Lagrange插值更好，三次样条插值曲线和原曲线在整个插值区间都基本处于重合状态，几乎没有肉眼可见的偏差.同样，由于三次样条插值的插值函数最高次数只有 3，在等距节点下也没有产生 Runge 现象.

对以上用两种插值方法对 Runge 函数和分段函数进行插值的结果进行分析可以得到以下结论及改进方向：（1）当插值多项式次数太高时，使用等距节点插值，会出现严重的 Runge 现象.如上述使用 Lagrange 函数对 Runge 函数进行等距 20 次插值，在插值区间两端都出现了剧烈的上下震荡，与原函数差别很大.

（2）降低插值多项式的次数能有效避免 Runge 现象.本实验中，三次样条插值法（最高次数为 3）都取得了较为理想的插值逼近效果，没有出现 Runge 现象，且在整个插值区间都与原函数的图像吻合的很好.

（3）在插值多项式次数很高时，若对插值节点进行适当选取，而不是使用等距节点，可以抑制 Runge 现象.例如,当在 20 次 Lagrange 插值中，使用切比雪夫多项式零点作为插值节点（节点两边密，中间疏），可有效消除了 Runge 现象.

综上，在实际运用中，为了取得较好的插值逼近效果，应尽量保证以下几点：不采用次数过高的插值多项式；适当选取插值节点；避免函数值突变，若不得已对存在不连续点的函数进行插值逼近，可以尝试分段插值，并将不连续点都处理到子区间的端点上，从而原函数在各子区间内分段连续，以便提高插值逼近的效果.

若有侵权,请联系作者删除

由于本人水平有限，如有理解或描述错误，还请各位批评指正.

作者邮箱: 517093978@qq.com

研究生期末考试

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

“十九届六中全会”全是考点！考试必背！(后有练习题) 上一篇

《机器学习》期末考试题下一篇