本文最后更新于：1 个月前

决策树一回归

[toc]

核心: 划分点选择 + 输出值确定.

一、概述

决策树是一种基本的分类与回归方法, 本文叙述的是回归部分.回归决策树主要指 CART (classification and regression tree)算法, 内部结点特征的取值为 “是”和“否”, 为二叉树结构.

所谓回归, 就是根据特征向量来决定对应的输出值.回归树就是将特征空间划分成若干单元, 每一个划分单元有一个特定的输出.因为每个结点都是“是”和“否”的判断, 所以划分的边界是平行于坐标轴的.对于测试数据, 我们只要按照特征将其归到某个单元, 便得到对应的输出值.

【例】左边为对二维平面划分的决策树, 右边为对应的划分示意图, 其中 \(c_{1}, c_{2}, c_{3}, c_{4}, c_{5}\) 是对应每个划分单元的输出.

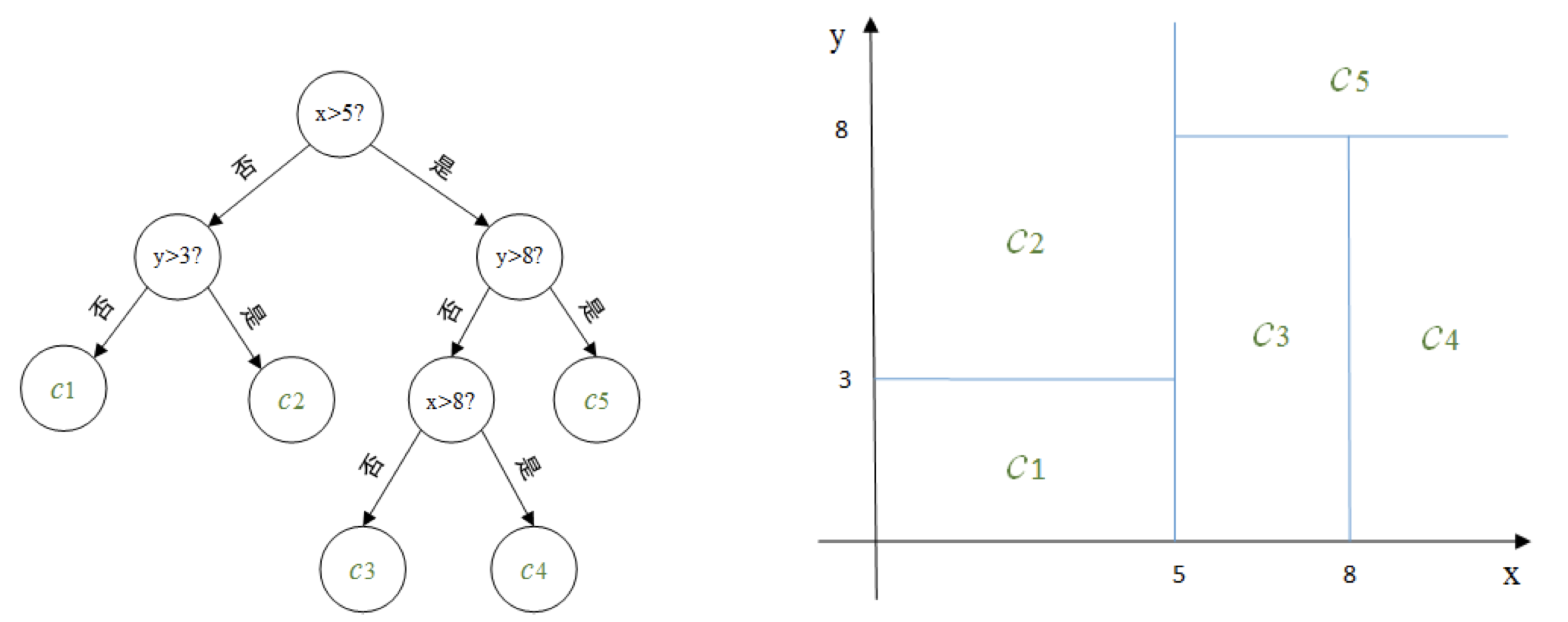
比如现在对一个新的向量 \((6,6)\) 决定它对应的输出.第一维分量 6 介于 5 和 8 之间, 第二维分量 6 小于 8 , 根据此决策树很容易判断 \((6,6)\) 所在的划分单元, 其对应的输出值为 \(c_{3}\).

划分的过程也就是建立树的过程, 每划分一次, 随即确定划分单元对应的输出, 也就多了一个结点.当根据停止条件划分终止的时候, 最终每个单元的输出也就确定了, 也就是叶结点.

二、回归树建立

既然要划分, 切分点怎么找? 输出值又怎么确定? 这两个问题也就是回归决策树的核心.

[切分点选择: 最小二乘法]; [输出值: 单元内均值].

1. 原理

假设 \(\mathrm{X}\) 和 \(\mathrm{Y}\) 分别为输入和输出变量, 并且 \(\mathrm{Y}\) 是连续变量, 给定训练数据集为 \(\mathrm{D}=\) \(\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots,\left(x_{N}, y_{N}\right)\right\}\), 其中 \(x_{i}=\left(x_{i}^{(1)}, x_{i}^{(2)}, \ldots, x_{i}^{(n)}\right)\) 为输入实例(特征向量), \(\mathrm{n}\) 为特征个数, \(\mathrm{i}=1,2, \ldots, \mathrm{N}, \mathrm{N}\) 为样本容量.

对特征空间的划分采用启发式方法, 每次划分逐一考察当前集合中所有特征的所有取值, 根据平方误差最小化准则选择其中最优的一个作为切分点.如对训练集中第 \(j\) 个特征变量 \(x^{(j)}\) 和它的取值 \(s\), 作为切分变量和切分点, 并定义两个区域 \(R_{1}(j, s)=\left\{x \mid x^{(j)} \leq s\right\}\) 和 \(R_{2}(j, s)=\) \(\left\{x \mid x^{(j)}>s\right\}\), 为找出最优的 \(\mathrm{j}\) 和 \(\mathrm{s}\), 对下式求解

\[ \min _{j, s}\left[\min _{c_{1}} \sum_{x_{i} \in R_{1}(j, s)}\left(y_{i}-c_{1}\right)^{2}+\min _{c_{2}} \sum_{x_{i} \in R_{2}(j, s)}\left(y_{i}-c_{2}\right)^{2}\right] \]

也就是找出使要划分的两个区域平方误差和最小的 \(j\) 和 \(s\).

其中, \(c_{1}, c_{2}\) 为划分后两个区域内固定的输出值, 方括号内的两个 \(\min\) 意为使用的是最优的 \(c_{1}\) 和 \(c_{2}\), 也就是使各自区域内平方误差最小的 \(c_{1}\) 和 \(c_{2}\), 易知这两个最优的输出值就是各自对应区域内 \(Y\) 的均值, 所以上式可写为

\[ \min _{j, s}\left[\sum_{x_{i} \in R_{1}(j, s)}\left(y_{i}-\widehat{c_{1}}\right)^{2}+\sum_{x_{i} \in R_{2}(j, s)}\left(y_{i}-\widehat{c_{2}}\right)^{2}\right] \]

其中 \(\widehat{C_{1}}=\frac{1}{N_{1}} \sum_{x_{i} \in R_{1}(j, s)} y_{i}, \widehat{c_{2}}=\frac{1}{N_{2}} \sum_{x_{i} \in R_{2}(j, s)} y_{i}\).

现证明一维空间中样本均值是最优的输出值 (平方误差最小):

给定一个随机数列 \(\left\{x_{1}, x_{2}, \ldots, x_{n}\right\}\), 设该空间中最优的输出值为 \(a\), 根据最小平方误差准则, 构造 \(a\) 的函数如下:

\[ \mathrm{F}(\mathrm{a})=\left(x_{1}-a\right)^{2}+\left(x_{2}-a\right)^{2}+\cdots+\left(x_{n}-a\right)^{2} \]

考察其单调性,

\[ F^{\prime}(a)=-2\left(x_{1}-a\right)-2\left(x_{2}-a\right)+\cdots-2\left(x_{n}-a\right)=2 n a-2 \sum_{i=1}^{n} x_{i} \]

令 \(F^{\prime}(a)=0\) 得, \(a=\frac{1}{n} \sum_{i=1}^{n} x_{i}\)

根据其单调性, 易知 \(\hat{a}=\frac{1}{n} \sum_{i=1}^{n} x_{i}\) 为最小值点.证毕.

找到最优的切分点 \((j, s)\) 后, 依次将输入空间划分为两个区域, 接着对每个区域重复上述划分过程, 直到满足停止条件为止.这样就生成了一棵回归树, 这样的回归树通常称为最小二乘回归树.

2. 算法叙述

输入: 训练数据集 D;

输出: 回归树 \(f(x)\).

在训练数据集所在的输入空间中, 递归地将每个区域划分为两个子区域并决定每个子区域上的输出值, 构建二叉决策树:

选择最优切分变量 \(\mathrm{j}\) 与切分点 \(\mathrm{s}\), 求解

\[ \min _{j, s}\left[\min _{c_{1}} \sum_{x_{i} \in R_{1}(j, s)}\left(y_{i}-c_{1}\right)^{2}+\min _{c_{2}} \sum_{x_{i} \in R_{2}(j, s)}\left(y_{i}-c_{2}\right)^{2}\right] \]

遍历变量 \(\mathrm{j}\), 对固定的切分变量 \(\mathrm{j}\) 扫描切分点 \(\mathrm{s}\), 选择使上式达到最小值的对 \((j, s)\).

用选定的对 \((j, s)\) 划分区域并决定相应的输出值:

\[ \widehat{c_{m}}=\frac{1}{N_{m}} \sum_{x_{i} \in R_{m}(j, s)} y_{i}, \quad \mathrm{x} \in R_{m}, \mathrm{~m}=1,2 \]

其中, \(R_{1}(j, s)=\left\{x \mid x^{(j)} \leq s\right\}, R_{2}(j, s)=\left\{x \mid x^{(j)}>s\right\}\).

继续对两个子区域调用步骤(1),(2), 直至满足停止条件.
将输入空间划分为 \(M\) 个区域 \(R_{1}, R_{1}, \ldots, R_{M}\), 生成决策树:

\[ \mathrm{f}(\mathrm{x})=\sum_{m=1}^{M} \widehat{c_{m}} I\left(x \in R_{m}\right) \]

其中 | 为指示函数, \(\mathrm{I}=\left\{\begin{array}{l}1 \text { if }\left(x \in R_{m}\right) \\ 0 \text { if }\left(x \notin R_{m}\right)\end{array}\right.\)

三、示例

(参考: [@一个拉风的名字 ](https://blog.csdn.net/weixin_40604987/article/details/79296427))

下表为训练数据集, 特征向量只有一维, 根据此数据表建立回归决策树.

x	1	2	3	4	5	6	7	8	9	10
y	5.56	5.7	5.91	6.4	6.8	7.05	8.9	8.7	9	9.05

选择最优切分变量 \(\mathrm{j}\) 与最优切分点 \(\mathrm{s}\) : 在本数据集中, 只有一个特征变量, 最优切分变量自然是 \(\mathrm{x}\) .接下来考虑 9 个切分点 \(\{1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5\}\) (切分变量两个相邻取值区间 \(\left[a^{i}, a^{i+1}\right.\) ) 内任一点均可), 根据式(1.2)计算每个待切分点的损失函数值:

损失函数为 (同式(1.2))

\[ L(j, s)=\sum_{x_{i} \in R_{1}(j, s)}\left(y_{i}-\widehat{c_{1}}\right)^{2}+\sum_{x_{i} \in R_{2}(j, s)}\left(y_{i}-\widehat{c_{2}}\right)^{2} \]

其中 \(\widehat{c_{1}}=\frac{1}{N_{1}} \sum_{x_{i} \in R_{1}(j, s)} y_{i}, \widehat{c_{2}}=\frac{1}{N_{2}} \sum_{x_{i} \in R_{2}(j, s)} y_{i}\).

计算子区域输出值

当 \(\mathrm{s}=1.5\) 时, 两个子区域 \(\mathrm{R} 1=\{1\}, \mathrm{R} 2=\{2,3,4,5,6,7,8,9,10\}, c_{1}=5.56\),

\[ c_{2}=\frac{1}{9}(5.7+5.91+6.4+6.8+7.05+8.9+8.7+9+9.05)=7.5 \]

同理, 得到其他各切分点的子区域输出值, 列表如下 | s | 1.5 | 2.5 | 3.5 | 4.5 | 5.5 | 6.5 | 7.5 | 8.5 | 9.5 | | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | | c_(1) | 5.56 | 5.63 | 5.72 | 5.89 | 6.07 | 6.24 | 6.62 | 6.88 | 7.11 | | c_(2) | 7.5 | 7.73 | 7.99 | 8.25 | 8.54 | 8.91 | 8.92 | 9.03 | 9.05 |

计算损失函数值, 找到最优切分点

当 \(\mathrm{s}=1.5\) 时,

\[ \begin{aligned} \mathrm{L}(1.5) &=(5.56-5.56)^{2}+\left[(5.7-7.5)^{2}+(5.91-7.5)^{2}+\cdots+(9.05-7.5)^{2}\right] \\ &=0+15.72 \\ &=15.72 \end{aligned} \]

同理, 计算得到其他各切分点的损失函数值, 列表如下

s	1.5	2.5	3.5	4.5	5.5	6.5	7.5	8.5	9.5
L(s)	15.72	12.07	8.36	5.78	3.91	1.93	8.01	11.73	15.74

易知, 取 \(s=6.5\) 时, 损失函数值最小.因此, 第一个划分点为 \((j=x, s=6.5)\).

用选定的对 \((j, s)\) 划分区域并决定相应的输出值:

划分区域为: \(R_{1}=\{1,2,3,4,5,6\}, R_{2}=\{7,8,9,10\}\)

对应输出值: \(c_{1}=6.24, c_{2}=8.91\)

调用步骤(1),(2), 继续划分:

\[ \text { 对 } R_{1} \text {, 取切分点 }\{1.5,2.5,3.5,4.5,5.5\} \text {, 计算得到单元输出值为 } \]

s	1.5	2.5	3.5	4.5	5.5
c_(1)	5.56	5.63	5.72	5.89	6.07
c_(2)	6.37	6.54	6.75	6.93	7.05

损失函数值为

s	1.5	2.5	3.5	4.5	5.5
L(s)	1.3087	0.754	0.2771	0.4368	1.0644

\(L(3.5)\) 最小, 取 \(s=3.5\) 为划分点.

后面同理.

生成回归树:

假设两次划分后即停止, 则最终生成的回归树为:

\[ \mathrm{T}=\left\{\begin{array}{cc} 5.72, & x \leq 3.5 \\ 6.75, & 3.5<x \leq 6.5 \\ 8.91, & x>6.5 \end{array}\right. \]

四. Python 实现

对第三部分例子的 python 实现及与线性回归对比. ### 程序源代码

# 开发者:    Leo 刘
# 开发环境: macOs Big Sur
# 开发时间: 2021/11/23 12:48 下午
# 邮箱  : 517093978@qq.com
# @Software: PyCharm
# ----------------------------------------------------------------------------------------------------------
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn import linear_model

# Data set
x = np.array(list(range(1, 11))).reshape(-1, 1)
y = np.array([5.56, 5.70, 5.91, 6.40, 6.80, 7.05, 8.90, 8.70, 9.00, 9.05]).ravel()

# Fit regression model
model1 = DecisionTreeRegressor(max_depth=1)
model2 = DecisionTreeRegressor(max_depth=3)
model3 = linear_model.LinearRegression()
model1.fit(x, y)
model2.fit(x, y)
model3.fit(x, y)

# Predict
X_test = np.arange(0.0, 10.0, 0.01)[:, np.newaxis]
y_1 = model1.predict(X_test)
y_2 = model2.predict(X_test)
y_3 = model3.predict(X_test)

# Plot the results
plt.figure()
plt.scatter(x, y, s=20, edgecolor="black",
            c="darkorange", label="data")
plt.plot(X_test, y_1, color="cornflowerblue",
         label="max_depth=1", linewidth=2)
plt.plot(X_test, y_2, color="yellowgreen", label="max_depth=3", linewidth=2)
plt.plot(X_test, y_3, color='red', label='liner regression', linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()
plt.show()

运行结果:

Decision Tree Regression

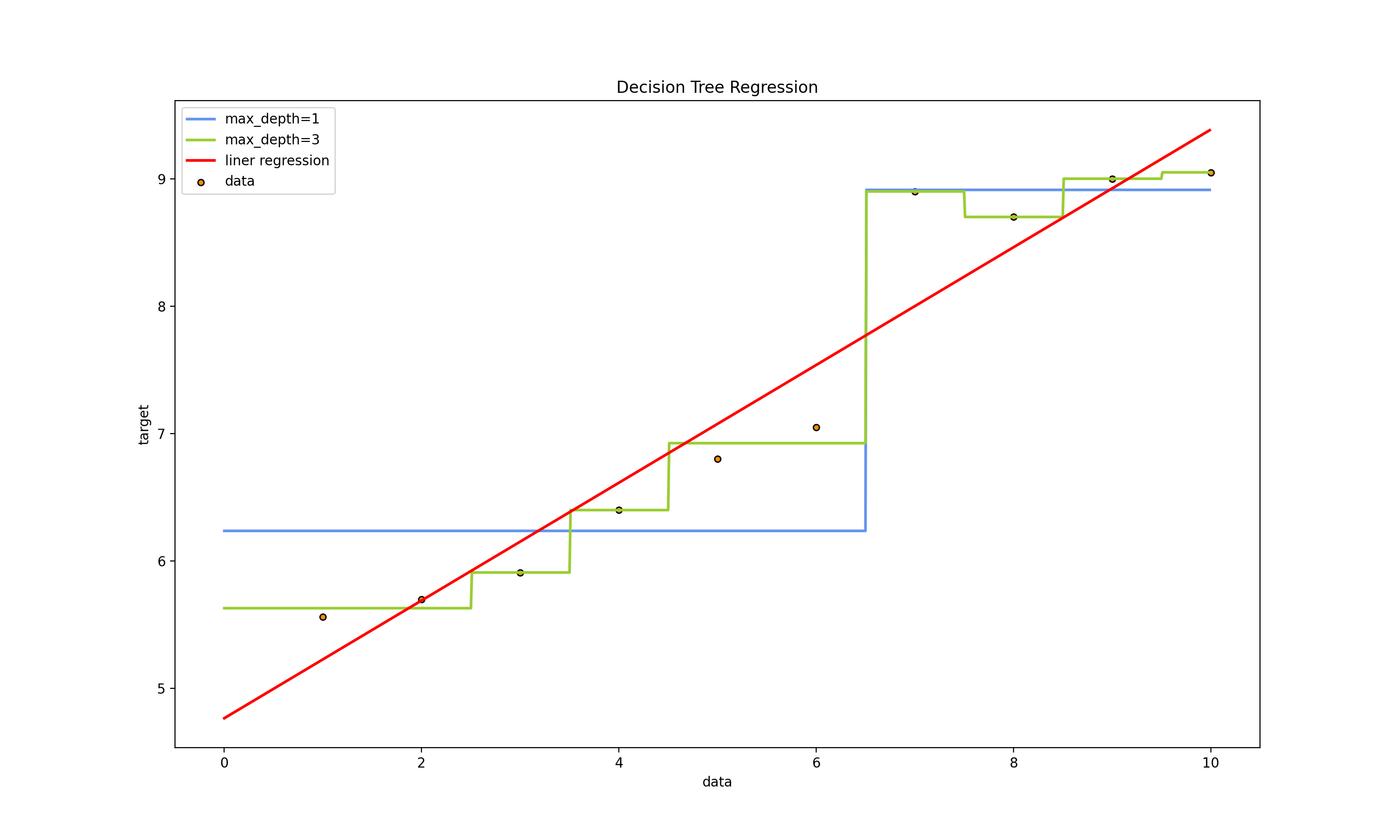
参考:

李航.《统计学习方法》.清华大学出版社.

周志华.《机器学习》.清华大学出版社.

CSDN.一个拉风的名字

笔记机器学习

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

FEALPy 求解 Poisson 方程上一篇

“十九届六中全会”全是考点！考试必背！(后有练习题) 下一篇