FEALPy：有限元方法求解一维扩散方程

有限元方法求解一维扩散方程

之前完成了 FEALPy 有限元求解 Poisson 方程 的数值算例, 通过湘潭大学王唯师兄的协助, 今天基于 FEALPy 运用有限元方法求解一个抛物型方程，为说明使用方法而又简单起见，于是理论部分专注于讨论下面这个一维的抛物型方程： \[ \begin{aligned} &\frac{\partial u}{\partial t}-a \frac{\partial^{2} u}{\partial x^{2}}=f(x, t), \quad(x, t) \in(0,1) \times(0, T] \\ &u(x, 0)=\psi(x), x \in[0,1] \\ &u(0, t)=u(1, t)=0, t \in[0, T] \end{aligned} \] ## 有限元方法推导

有限元方法相对于有限差分方法的一个巨大优势在于：对于复杂的几何区域, 网格可以画得非常 随意, 而有限差分法的格式需要建立在规则的网格上.

幸运的是, 复杂区域只存在于空间上, (通常) 并没有“复杂的时间区域” 这一说法, 毕竟时间是一维的, 一维空间上的连通区域都相似于直线、线段、射线之一, 都是相当简单的几何.

也就是说, 在时间轴上或许可以继续沿用有限差分法, 而在空间上采用有限元的方法. 回忆一下用有限元求解的 hello world 模型, 椭圆型问题: \[ \begin{aligned} &-a \frac{\partial^{2} u}{\partial x^{2}}=f(x), \quad x \in(0,1) \\ &u(0)=u(1)=0 \end{aligned} \] 是将其转化为弱形式, 找一个 \(u \in H_{0}^{1}(0,1)\), 使得: \[ a \int_{0}^{1} v^{\prime} u^{\prime} d x=\int_{0}^{1} f v d x \] 对任意的 \(v \in H_{0}^{1}(0,1)\) 成立来达成的.

具体而言, 是构造一组基于空间的基函数, 使得解在基函数构成的空间中被逼近, 也就是 \[ u(x)=\sum_{i=0}^{N} c_{i} \phi_{i}(x) \] 每一个基函数的系数是固定的, 而对于今天这个时间依赖的抛物问题, 那就构造随时间变化的系数来表示好了, 也就是 \[ u(x, t)=\sum_{i=0}^{N} c_{i}(t) \phi_{i}(x) \] 再用弱形式写一下, 就是找到上面的 \(\mathrm{u}\), 使得对任意 \(v \in H_{0}^{1}(0,1)\), 都有 \[ \int_{0}^{1} v(x) \frac{\partial u}{\partial t} d x-a \int_{0}^{1} v(x) \frac{\partial^{2} u}{\partial x^{2}} d x=\int_{0}^{1} f(x, t) v(x) d x \] 运用分部积分公式换一换, 得到 \[ \int_{0}^{1} v(x) \frac{\partial u}{\partial t} d x+a \int_{0}^{1} v^{\prime}(x) \frac{\partial u}{\partial x} d x=\int_{0}^{1} f(x, t) v(x) d x \] 然后由于对于固定的t, 上式的成立也等价于 \[ \sum_{i=0}^{N}\left(c_{i}^{\prime}(t) \int_{0}^{1} \phi_{j}(x) \phi_{i}(x) d x+a \cdot c_{i}(t) \int_{0}^{1} \phi_{j}^{\prime}(x) \phi_{i}^{\prime}(x) d x\right)=\int_{0}^{1} f(x, t) \phi_{i}(x) d x \] 写成矩阵形式 \[ A C^{\prime}(t)+a K C(t)=F(t) \] 其中 1. \(C(t)=\left[c_{0}(t), c_{1}(t), \cdots, c_{N}(t)\right]\), 基函数系数 2. \(A=\left[\int_{0}^{1} \phi_{i} \phi_{j} d x\right]_{i j}\), 称为质量矩阵 3. \(K=\left[\int_{0}^{1} \phi_{i}^{\prime} \phi_{j}^{\prime} d x\right]_{i j}\), 是熟悉的全局刚度阵 4. \(F(t)=\left[\int_{0}^{1} \phi_{i}(x) f(x, t) d x\right]_{i}\), 是载荷向量

然后上面的式子就是更久之前所学习的常微分方程了, 当然这个常微分方程的求解还需要初值条件： \[ A C(0)=F(0) \] 其中 \(F(0)=\left[\int_{0}^{1} \phi_{i}(x) \psi(x) d x\right]_{i}^{T}\), 是个向量.

至此, 就可以开始求解方程了.

差分格式的介入

空间的处理交给了有限元方法, 而时间可以交给差分格式, 为了使用差分格式, 直接将时间 \([0, T]\) 离散为 \(t_{0}, t_{1}, \cdot, t_{M}\) .然后再用

向前 Euler 格式, 得到 \[ \begin{array}{r} A \frac{C_{k+1}-C_{k}}{\Delta t}+a K C_{k}=F\left(t_{k}\right) \\ C_{0}=A^{-1} F_{0} \end{array} \] 或者向后 Euler 格式 \[ \begin{array}{r} A \frac{C_{k}-C_{k-1}}{\Delta t}+a K C_{k}=F\left(t_{k}\right) \\ C_{0}=A^{-1} F_{0} \end{array} \] 或者二阶精度的中心 Euler 格式 \[ \begin{array}{r} A \frac{C_{k+1}-C_{k}}{\Delta t}+a K \frac{C_{k}+C_{k+1}}{2}=F\left(t_{k+\frac{1}{2}}\right) \\ C_{0}=A^{-1} F_{0} \end{array} \] 或者按需选取别的格式...

还需要处理的就是两处数值积分了 \(F(t)\) 和 \(F_{0}\) 了, 如同往常, 采用Gauss积分公式求解即可.

数值算例

考虑二维抛物方程：

\[ \begin{cases}\frac{\partial u(\vec{x}, t)}{\partial t}-\Delta u(\vec{x}, t)=(2\pi^2-1)\sin (\pi x_1)\sin (\pi x_2) e^{-t}, & (\vec{x}, t) \in \Omega \times (0,1]\\ u(\vec{x}, t)=\sin (\pi x_1)\sin (\pi x_2) e^{-t}, & (\vec{x}, t) \in \Omega\times 0\\ u(\vec{x}, t)=\sin (\pi x_1)\sin (\pi x_2) e^{-t}, & (\vec{x}, t) \in \partial \Omega\times[0,1]\end{cases} \]

其中, 空间区域 \(\Omega:=[0,1]\times[0,1]\), 其真实解为 \(u(\vec{x}, t)=\sin (\pi x_1)\sin (\pi x_2) e^{-t}\) .

下面演示基于 FEALPy 求解这个算例的过程.

from fealpy.pde.parabolic_model_2d import SinSinExpData
from fealpy.mesh import MeshFactory as MF
from fealpy.functionspace import LagrangeFiniteElementSpace
from fealpy.boundarycondition import DirichletBC
from fealpy.decorator import cartesian
from scipy.sparse.linalg import spsolve
import matplotlib.pyplot as plt

t_list = []
error = []
# 创建 PDE 模型
pde = SinSinExpData()
# 创建网格
domain = [0, 1, 0, 1]
mesh = MF.boxmesh2d(domain, nx=5, ny=5, meshtype='tri')
# 时间离散
timeline = pde.time_mesh(0, 1, 100)
# 建立 Lagrange 有限元函数空间
space = LagrangeFiniteElementSpace(mesh, p=2)
# 时间步进求解
for i in range(100):
    t = timeline.next_time_level()
    # 创建 Dirichlet 边界条件对象
    @cartesian
    def dirichlet(p):
        return pde.dirichlet(p, t)
    bc = DirichletBC(space, dirichlet)
    # 创建离散代数系统
    uh = space.function()
    A = space.stiff_matrix()
    @cartesian
    def source(p):
        return pde.source(p, t)
    F = space.source_vector(source)
    # 处理边界条件
    A, F = bc.apply(A, F, uh)
    # 求解离散代数系统
    uh[:] = spsolve(A, F)

    # 计算 L2 误差并保存
    @cartesian
    def solution(p):
        return pde.solution(p, t)
    L2Error = space.integralalg.L2_error(solution, uh)
    # print('t:/t', t, '/tL2Error:', L2Error)
    t_list.append(t)
    error.append(L2Error)
    # 前进一层
    timeline.forward()
# 绘制时间方向 L2 误差
plt.xlabel('t')
plt.ylabel('error')
plt.title('L2Error')
plt.plot(t_list, error)
plt.show()
# 绘制数值解图像和网格图像
fig = plt.figure()
axes = fig.add_subplot(1, 2, 1, projection='3d')
uh.add_plot(axes, cmap='rainbow')
axes = fig.add_subplot(1, 2, 2)
mesh.add_plot(axes)
plt.show()

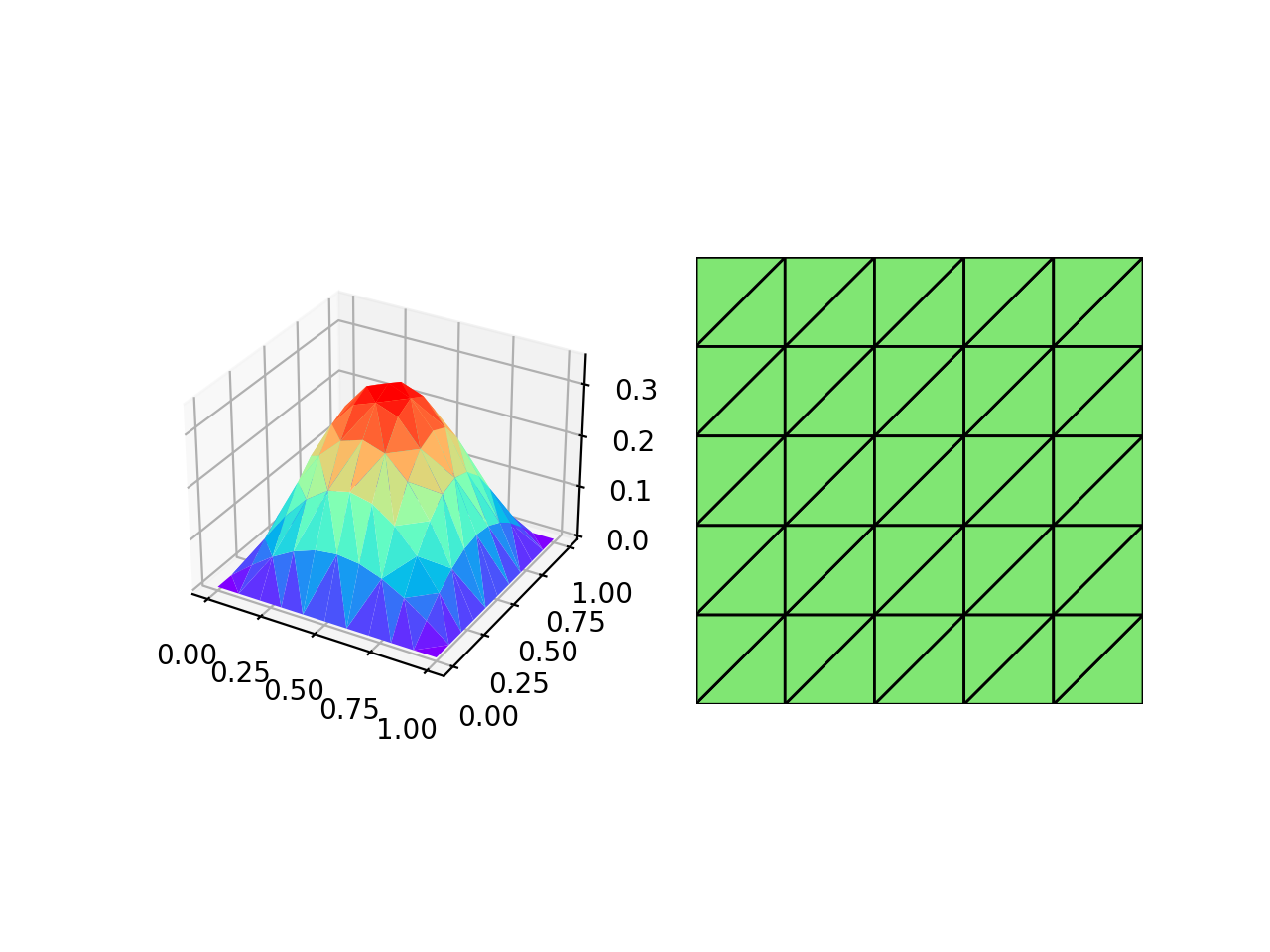
数值结果: 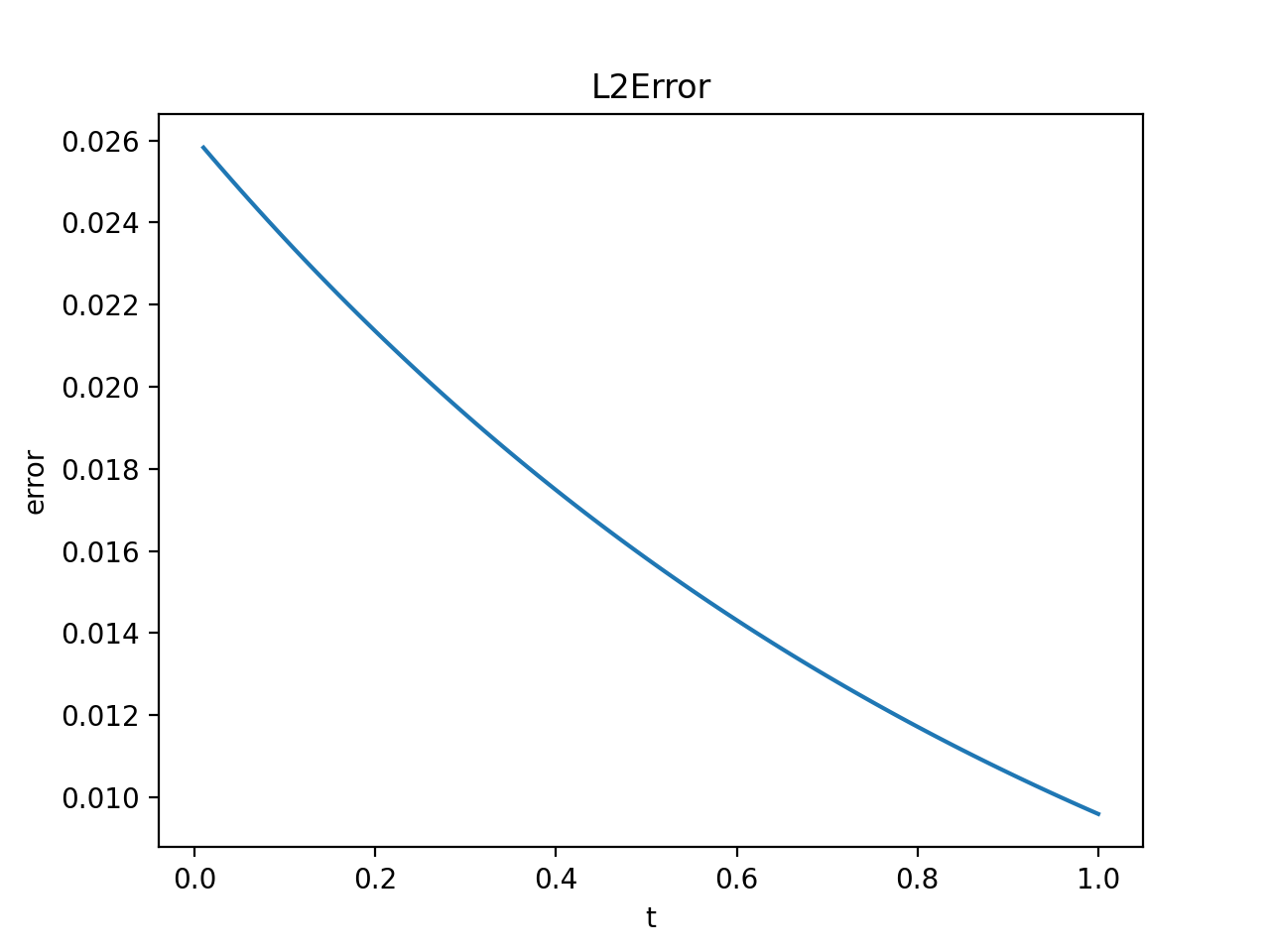>本人水平有限, 若有错误, 欢迎联系批评指正 > >作者邮箱: turingscat@126.com